Оценить точность построенной модели с использованием средней относительной ошибки аппроксимации

По столбцам исходных данных (Таблица 2) и полученных данных 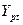(Таблица 4) рассчитаем остатки

Получим следующие результаты

Таблица6

E(t)	отн.погр.	E(t)	отн.погр.
0,09	0,29	-0,94	2,67
-0,03	0,08	2,43	5,79
-1,14	2,42	-0,15	0,29
0,68	2,20	-0,29	0,47
-0,11	0,31	0,30	0,76
0,10	0,22
1,79	3,32
-1,20	3,62
-0,32	0,87
0,06	0,12
-0,60	1,05

Для проверки точности рассчитаем относительную погрешность каждого уровня

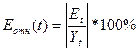
используя функции табличного процессора Microsoft Excel (Мастер функции/Категория – Математические/ABS) (Таблица 6).

По полученным результатам определим среднее значение с помощью функций табличного процессора Microsoft Excel (Мастер функции/Категория – Статистические/СРЗНАЧ).

Средняя относительная ошибка аппроксимации составляет 1,53%, которая меньше 5% => модель имеет высокую точность.

3. Оценить адекватность построенной модели на основе исследования:

- случайности остаточной компоненты по критерию пиков;

- независимости уровней ряда остатков по d-критерию (критические значения d1=1,10 и d2=1,37) и по первому коэффициенту автокорреляции при критическом значении r кр =0,32.

- нормальности распределения остаточной компоненты по R/S-критерию с критическими значениями от 3 до 4,21.

Для проверки случайности остатков рассмотрим график остатков

График 1

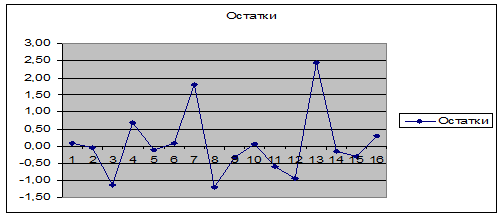
По графику найдем количество поворотных точек – это точки максимума и минимума. => Р=9.

Определим по формуле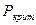

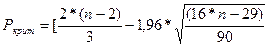
При n=16 получим

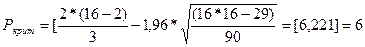
Так как Р=9> 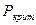=6 => свойство случайности остатков выполняется.

Проверка независимости остатков по d – критерию

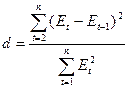
Подготовим 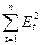, 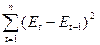с помощью функций табличного процессора Microsoft Excel СУММКВ и СУКВРАЗН (Мастер функции/Категория – Математические/СУММКВ; Мастер функции/Категория – Математические/СУММКВРАЗН) => 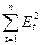=13,89; 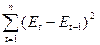=36,86 =>

=>

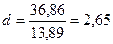
Так как d =2,65 > 2, то величину d уточним, т.е. d =4-2,65=1,35

Критические значения равны 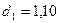и 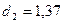(по условию задачи); d =1,35> 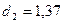, т.е. 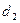< d <2 => уровни ряда остатков является независимыми.

Проверим отсутствие автокорреляция по первому коэффициенту автокорреляции.

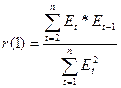
Подготовим с помощью табличного процессора Microsoft Excel СУММПРОИЗВ (Мастер функции/Категория – Математические/СУММПРОИЗВ) => = -4,59 => .

Критическое значение 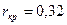(по условию задачи).

=> свойство независимости остаточной компоненты не выполняется.

Рассчитаем значения R/S по формуле

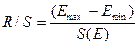
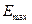и найдем с помощью табличного процессора Microsoft Excel МАКС и МИН (Мастер функции/Категория – Статистические/МАКС; Мастер функции/Категория – Статистические/МИН) => 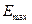=2,43; =-1,20

S(E) найдем с помощью табличного процессора Microsoft Excel (Мастер функции/Категория – Статистические/СТАНДОТКЛОН) => S(E) =0,96

Получим

Полученное значение R/S сравним с табличными значениями [3;4,21] => R/S =3,78 входит в критический интервал => свойство нормального распределения остатков выполняется.

Таким образом, по точности модель удовлетворительна, но не является адекватной, так как не выполняется свойство независимости остатков. Прогноз по этой модели проводить нецелесообразно.

Дата добавления: 2015-03-31