
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Формула Тейлора. Формула Маклорена
|
|
|
|
Производные и дифференциалы высших порядков.
Если для функции y=f(x) определена производная у(к-1) порядка (к-1), то производную у(к) порядка к (при условии ее существования) определяют как производную от производной порядка (к-1), т.е. у(к) = (у(к-1))′. В частности, у’’=(y’)’- производная второго порядка, y’’’=(y’’)’ – третьего и т.д.
Дифференциалы высших порядков ф-и y=f(v) последовательно определяются таким образом:
d2y=d(dy) – диф-л 2-го порядка
d3y=d(d2y)…
dny=d(d n-1 y) - диф-л n-го порядка
теорема Тейлора.
Пусть функция f (x) имеет в точке x = a и некоторой ее окрестности производные порядка n+ 1. Тогда между точками a и x a найдется такая точка  , что справедлива следующая формула:
, что справедлива следующая формула:
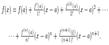
|
Формула (10) называется формулой Тейлора, а выражение
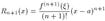
представляет остаточный член в форме Лагранжа. Заметим, что если функция f (n+ 1)(x) ограничена в окрестности точки a, тогда остаточный член является бесконечно малой при x a более высокого порядка, чем (x-a) n. Таким образом, остаточный член можно записать в виде
Rn+ 1(x) = o ((x-a) n) при x a.
Данная форма записи остаточного члена называется формой Пеано.
Формулой Маклорена называется формула Тейлора при a = 0:

|
Остаточный член в форме Пеано для формулы Маклорена имеет вид
Rn+ 1 = o (xn) при x 0.
 Приведем разложения некоторых элементарных функций по формуле Маклорена
Приведем разложения некоторых элементарных функций по формуле Маклорена
29. признак монотонности дифференцируемой функции:
Промежутки монотонности ф-ции совпадают с промежутками постоянного знака её производной
30. определение локального экстремума функции одной переменной:
Точка x0 называется точкой локального max [min] ф-ции f(x), если для всех x из некоторой окрестности точки x0 выполняется неравенство 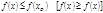
Локальный max и min объединяются общим названием локальны экстремум.
31. необходимое условие локального экстремума функции одной переменной:
Для того, чтобы дифференцируемая ф-ция f(x) имела в точке x0 локальный экстремум необходимо, чтобы в этой точке выполнялось равенство 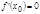 . Если
. Если 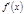 при переходе через точку х0 меняет знак с + на – (с – на +), то х0 – это локальный максимум (минимум).
при переходе через точку х0 меняет знак с + на – (с – на +), то х0 – это локальный максимум (минимум).
.
32. точка перегиба функции:
пусть функция f(x) непрерывна в точке х0. Точка х0 называется точкой перегиба, если при переходе через нее кривая меняет направление выпуклости.
33. необходимое условие точки перегиба:
пусть функция f(x) непрерывна в точке х0. Точка х0 называется точкой перегиба, если при переходе через нее кривая меняет направление выпуклости (слева и справа от х0 знаки второй производной различны)
34. определение асимптот графика функций:
Асимптота графика функций y=f(x) - это прямая, расстояние до которой от точки (x,y) графика функций y=f(x) стремится к нулю, если хотя бы одна из координат (x,y) стремится к бесконечности. Асимптоты бывают вертикальными, наклонными и горизонтальными.
35. определение первообразной для функций y=f(x) на промежутке X:
Пусть задана функция f(x) на интервале (a,b). функция F(x) называется первообразной для функции f(x) на интервале (a,b), если F`(x)= f(x)для всех x принадлежащих (a,b).
36. определение неопределенного интеграла:
Совокупность всех первообразных функций f(x) называется неопределенным интегралом и обозначается («интеграл эф от икс дэ икс»).
37. свойства неопределенного интеграла:
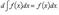
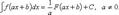
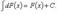
38.Формула замены переменной в неопределенном интеграле.
Если интеграл нельзя найти непосредственно, то в некоторых случаях можно применить метод замены переменной, положив х=ф(t), где ф(t)- непрерывно дифференцируемая монотонная функция. Справедливая формула замены переменной: 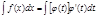
39.Формула интегрирования по частям для неопределенного интеграла.
Пусть u(x) и v(x) – две дифференцируемые функции на промежутке Х. Тогда на Х выполняется формула интегрирования по частям
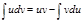
40.Определение определенного интеграла Римана.
Если функция y=f(x) интегрируема на отрезке [a;b], то единственное число, разделяющее эти два множества называют определенным интегралом функции y=f(x) по отрезку[a;b] и обозначают следующим образом: 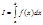
41. Достаточное условие интегрируемости.
Функция y=f(x) называется интегрируемой на этом отрезке, если существует единственное число I, разделяющее множества нижних и верхних сумм Дарбу для всевозможных разбиений отрезка [a;b].
42. Геометрический смысл определенного интеграла: определенный интеграл равен площади криволинейной трапеции ограниченной линиями x=a,x=b при b>a, осью Ох и графиком неотрицательной непрерывной ф-цииy=f(x)
43.Свойства определенного интеграла.
1) 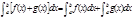 . 2)
. 2) 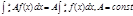
3)  4)
4) 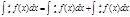 ,для любых a,b,c. 5)Если f(x)≤g(x) отрезке [a,b], то
,для любых a,b,c. 5)Если f(x)≤g(x) отрезке [a,b], то 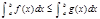 6)Если на отрезки [a,b] выполняется неравенства
6)Если на отрезки [a,b] выполняется неравенства 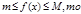
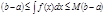 ( оценка интеграла). 7)Теорема о среднем. Для непрерывной на отрезке[a,b] функция y=f(x) найдется точка С принадлежащая [a,b],что
( оценка интеграла). 7)Теорема о среднем. Для непрерывной на отрезке[a,b] функция y=f(x) найдется точка С принадлежащая [a,b],что 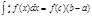 .
.
44. Формула Ньютона-Лейбница.
Для нахождения определенного интеграла для функции f(x), интегрируемой на отрезке[a,b ]: 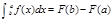 , гдеF(x)- любая первообразная для функции f(x) на[a,b].
, гдеF(x)- любая первообразная для функции f(x) на[a,b].
45.Формула замены переменной в определенном интеграле.
Пусть в определенном интеграле 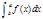 с непрерывной подынтегральной функцией f(x) производят замену переменной x=
с непрерывной подынтегральной функцией f(x) производят замену переменной x=  (t), при чем функция
(t), при чем функция 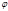 (t) непрерывно дифференцируема на отрезке [
(t) непрерывно дифференцируема на отрезке [ 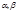 ] и
] и 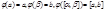 тогда справедливо равенство
тогда справедливо равенство 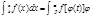 (t)dt.
(t)dt.
46.Формула интегрирование по частям для определенного интеграла.
Пусть u(x) и v(x)-две непрерывно дифференцируемые функции на отрезке [a,b]. Тогда выполняется формула интегрирования по частям 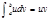
 │
│ 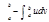
47. Определение несобственного интеграла с бесконечно верхним пределом.
Если существует конечный предел 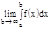 , тоэтот предел называется несобственным интегралом с бесконечно верхним пределом пределом от функции f(x)и обозначается
, тоэтот предел называется несобственным интегралом с бесконечно верхним пределом пределом от функции f(x)и обозначается 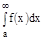 .
.
48.Определение несобственного интеграла с бесконечно нижним пределом.
Еслисуществует конечныйпредел 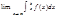 , то этот предел называется несобственным интегралом с бесконечно нижним пределом от функции f(x)и обозначается
, то этот предел называется несобственным интегралом с бесконечно нижним пределом от функции f(x)и обозначается 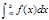 .
.
49.Определение несобственного интеграла от неограниченной функции на ограниченном промежутке.
Если функция f(x) определена при 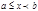 , интегрируема на любом отрезке
, интегрируема на любом отрезке 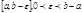 и не ограничена слева от точки b, то по определению полагают
и не ограничена слева от точки b, то по определению полагают 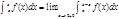 Аналогично, если функция f(x) не ограничена справа от точки а, то
Аналогично, если функция f(x) не ограничена справа от точки а, то 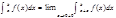 . Наконец, если функция в окрестности внутренней точки с отрезка [a,b]не ограничена, то по определению
. Наконец, если функция в окрестности внутренней точки с отрезка [a,b]не ограничена, то по определению 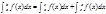 .
.
50. Расстояние в Rⁿ. Свойства расстояния.
В пространстве Rⁿ, где n>3, о расстоянии можно говорить лишь в условном смысле, так как точки в Rⁿ не имеют непосредственного геометрического истолкования. Расстояние определяется формулой:
ρ (p,q)= │p-q│=√(x1’- x1”)²+…+(xⁿ’-xⁿ”)²
, где p=(x1’, x2’, …, xⁿ’) и q=(x1”, x2”, …, xⁿ”) – две произвольные точки из Rⁿ.
Свойства:
1) ρ (p,q)>0, елси p ≠ q, и ρ (p,p)=0;
2) ρ (p,q)= ρ (q,p);
3) ρ (p,q)+ ρ (q,r)>= ρ (p,r), каковы бы ни были точки p,q и r. (свойство треугольника).
51. Окрестность точки в Rⁿ.
Пусть pₒ- точка в Rⁿ и ε – положительное число. Открытым шаром, или просто шаром радиуса ε с центром в pₒ называется множество всех точек, расстояние которых от pₒ меньше ε:
{p € Rⁿ │ ρ (pₒ,p)< ε}.
Шар радиуса ε с центром pₒ обозначается B(pₒ, ε) или U3(pₒ). Множество U3(pₒ) называют
ε–окрестностью точки pₒ.
Внутренние и граничные точки множества:
Пусть Х – множество в пространстве Rⁿ. Точка р называется:
-Внутренней точкой множества Х, если она содержится вместе с некоторой своей
ε–окрестностью;
-Внешней точкой по отношению к Х, если она является внутренней для дополнения Х в Rⁿ;
-Граничной точкой для Х, если она не является ни внутренней ни внешней точкой для Х, иначе говоря, если любая ее окрестность содержит как точки, принадлежащие Х, так и точки, не принадлежащие Х.
52. Открытые и замкнутые множества.
Множество X называется открытым, если все его точки внутренние.
Множество X называется закрытым, если оно содержит все свои граничные точки.
53. Изолированные и предельные точки множества.
Пусть X - множество в Rn. Точка p0 называется предельной для X, если в любой
ε-окрестности точки p0 имеются точки множества X, отличные от p0.
При этом сама точка p0 может как принадлежать, так и не принадлежать множеству X.
Точка p0 Î X называется изолированной точкой множества X, если у нее существует
ε-окрестность, в которой никаких других точек из X, кроме p0, нет.
Ясно, что любая точка множества Х является либо изолированной, либо предельной
для Х.
54. Ограниченные множества.
Множество X  Rn называется ограниченным, если оно целиком содержится в некотором шаре.
Rn называется ограниченным, если оно целиком содержится в некотором шаре.
Нетрудно показать, что ограниченность множества Х означает, что существует такое число C>0, что координаты любой точки p=(x1,x2,…,xn) из Х по модулю не превосходят С: |x1| 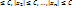 .
.
55. Сходимость последовательности точек в Rn, ее эквивалентность покоординатной сходимости.
Пусть 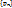 – последовательность точек в Rn. Мы говорим, что эта последовательность сходится к точке p0, если числовая последовательность
– последовательность точек в Rn. Мы говорим, что эта последовательность сходится к точке p0, если числовая последовательность 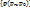 имеет предел 0.
имеет предел 0.
Пусть p1=(x1,y1), p2=(x2,y2),…- последовательность точек в  . Мы скажем, что эта последовательность сходится к точке p0=(x0,y0), если числовая последовательность x1,x2,… сходится к числу x0, а числовая последовательность y1,y2,… - к числу y0.
. Мы скажем, что эта последовательность сходится к точке p0=(x0,y0), если числовая последовательность x1,x2,… сходится к числу x0, а числовая последовательность y1,y2,… - к числу y0.
56. Функция нескольких переменных.
Числовая ф-ция n переменных характеризуется тем, что областью ее определения является подмножество Х пространства Rn, n>1В этом случае значение аргумента х представляет собой точку (х1,х2,..хn).
57. Поверхности (линии) уровня функции нескольких переменных.
Линией уровня функции называют линию f(x,y)=C на координатной плоскости, в точках которой функция f принимает постоянное значение C.
При n>2 следует говорить не о линиях, а о множествах уровня. Множество уровня имеет уравнение f(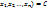 и истолковывается как “ поверхность” в
и истолковывается как “ поверхность” в 
58. Предел функции нескольких переменных.
Пусть на множестве X  Rn задана функция f(p) и пусть p0 – предельная точка для Х. Число a называется пределом функции f в точке p0, если для любой сходящейся к p0 последовательности
Rn задана функция f(p) и пусть p0 – предельная точка для Х. Число a называется пределом функции f в точке p0, если для любой сходящейся к p0 последовательности 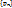 , где все pn
, где все pn  p0, соответствующая числовая последовательность
p0, соответствующая числовая последовательность 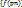 сходится к числу а.
сходится к числу а.
Запись: 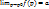 , или в координатной форме:
, или в координатной форме: 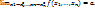
59. Непрерывность функции нескольких переменных.
Функция f(p), определенная на множестве X  Rn, называется непрерывной
Rn, называется непрерывной
в точке р0 Î X, если  , или же, если p0 – изолированная точка множества Х.
, или же, если p0 – изолированная точка множества Х.
Функция f(p), определенная на множестве X  Rn, называется непрерывной на этом множестве, если она непрерывна в каждой точке множества Х.
Rn, называется непрерывной на этом множестве, если она непрерывна в каждой точке множества Х.
60. Свойства функций, непрерывных на замкнутом ограниченном множестве: ограниченность, достижение наибольшего и наименьшего значений.
Если числовая функция f от n переменных задана на ограниченном и замкнутом множестве Х  Rn, то она ограничена на этом множестве.
Rn, то она ограничена на этом множестве.
Если числовая функция f от n переменных задана на ограниченном и замкнутом множестве Х  Rn, то существует точка p0 Î X, в которой f принимает свое наименьшее значение, и точка q0 Î X, в которой f принимает свое наибольшее значение на Х.
Rn, то существует точка p0 Î X, в которой f принимает свое наименьшее значение, и точка q0 Î X, в которой f принимает свое наибольшее значение на Х.
61. Частные производные функции нескольких переменных.
Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения частного приращения функции к приращению соответствующей независимой переменной, когда это приращение стремится к нулю.
Частные производные функции z=f(x,y) в точке (x0,y0) обозначаются так:
z’x, dz/dx, f’x(x0,y0) – производная по x;
z’y, dz/dy, f’y(x0,y0) – производная по y.
62.Дифференцируемость функции нескольких переменных Ф-цияz=f(x,y) называетсядифференцируемойвточке (x0,y0), еслиееполноеприращениеможнопредставитьввиде: ∆z=f(x,y)-f(x0,y0)=f’x(x0,y0)∆x+ f’y(x0,y0)∆y+eρ, либо ∆z=dz+ eρ, гдее=е(∆x,∆y)- ф-циябесконечномалаяпри ∆x→0,∆y→0; ρ=√((∆x)2+∆y2)-расстояниеотточки (x,y) доточки(x0,y0)
63. Дифференциал функции нескольких переменных. Полный дифференциал ф-циивыполняет роль линейного приближения и определяется как сумма произведений частных производных ф-ции на приращения независимых переменных: dz=z’x∆x+z’y∆y
64. Достаточное условие дифференцируемости функции нескольких переменных. Если частные производные f’x(x,y) и f’y(x,y) определены в окрестности точки (x0,y0), то ф-цияz=f(x,y) дифференцируема в этой точке
65. Непрерывность дифференцируемой функции. Если ф-цияz=f(x,y)дифференцируема в точке (x0,y0), то она непрерывна в этой точке.
66. Однородные функции. Ф-ция z(x;y) называется однородной степени α, если для любой точки (х;у) из области определения и переменной t выполняется равенство z(tx;ty)= tα z(x;y).
Пусть D из Rn – область в Rn, содержащая с каждой своей точкой (x1, x2, …., xn) и все точки вида (tx1, tx2, …., txn) при t>0 ф-ция f(x1, x2, …., xn) с такой областью определения D называется однородной степени λ, если для любого t>0 выполнятся равенство f (tx1, tx2, …., txn)=tλ f(x1, x2, …., xn).
67. Формула Эйлера для однородной функции. f’x(tx, ty)x+f’y(tx, ty)y=λtλ-1f(x,y)
Положив здесь t=1,получим формулу Эйлера:
f’x(x, y)x+f’y(x, y)y=λf(x,y)
68.Производная сложной функции. Сложной функцией называется такая функция аргумент которой представляет собой ещё одну функцию.
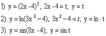
Правило вычисления производной сложной функции: Производная сложной функции равна произведению производной основной функции на производную вспомогательной
69..Производная по направлению.
Производной ф-ции f(x,y) в точке (x0,yo) по направлению ℮ называется предел
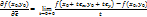
70. Градиент. Свойства градиента Градиентом ф-ции z= f(x,y) в точке M(x,y) называется вектор, координаты которого равны соответствующим частным производным, взятым в точке M(x,y).
Grad f(M)=(f’x(M),f’y(M)). Градиент указывает направление наискорейшего роста ф-ции, а максимальная скорость роста равна модулю градиента.
│Gradf(M)│=δf(M)/δe
Положимѱ(t)=f(p+tv), p,vϵRn, тогдаѱ’(0)=(gradf(p),v)
Градиент ф-цииgradf(M) является вектором нормали касательной к линии уровня в точке М
Градиент ф-цииf(x,y,z) является вектором нормали касательной плоскости к поверхности уровня ф-ции в точке М
71. Частные производные высших порядков. Частные производные от функций f’x(x,y) и f’y(x,y) называют частными производными второго порядка от ф-цииf(x,y).Частные производные от частных производных второго порядка называют частными производными третьего порядка от ф-ции. Частные производные второго порядка z’’xyиz’’yxназывают смешанными частными производными.
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 810; Нарушение авторских прав?; Мы поможем в написании вашей работы!