Средние величины. Среди обобщающих показателей, характеризующих статистические совокупности, большое значение имеют средние величины

Среди обобщающих показателей, характеризующих статистические совокупности, большое значение имеют средние величины.

Применение метода средних величин в статистических исследованиях имеет глубокую историю, уходящую своими корнями в период формирования и становления самой статистической науки, период, который был ознаменован первыми попытками подойти к проблеме изучения больших массивов данных комплексно, применяя аналитические обобщения для формулировки значимых для исследователя выводов.

Средняя величина – это обобщающая характеристика множества индивидуальных значений некоторого количественного признака.

Совокупность, изучаемая по количественному признаку, состоит из индивидуальных значений; на них оказывают влияние как общие причины, так и индивидуальные условия. В среднем значении отклонения, характерные для индивидуальных значений, погашаются, а в средней отчетливо выявляется основная тенденция развития.

Важнейшая особенность средней величины – в том, что она относится к единице изучаемой совокупности и через характеристику единицы характеризует всю совокупность в целом.

Основные свойства средней величины:

1. Она обладает устойчивостью, что позволяет выявлять закономерности развития явлений. Средняя величина облегчает сравнение двух совокупностей, обладающих различной численностью.

2. Она помогает характеризовать развитие уровня явления во времени.

3. Она помогает выявить и охарактеризовать связь между явлениями.

Средняя всегда дает обобщенную характеристику лишь по одному признаку. Каждая же единица совокупности имеет много признаков. Поэтому необходимо рассчитывать систему средних, чтобы охарактеризовать явление со всех сторон.

Расчет средних величин производится по правилам, которые разрабатываются математической статистикой. Задача общей теории статистики – дать смысловую, преимущественно экономическую интерпретацию результатам расчетов, произведенных по формулам.

В статистике выделяют несколько видов средних величин:

1. По наличию признака-веса:

а) простая средняя величина;

б) взвешенная средняя величина.

2. По форме расчета:

а) средняя арифметическая величина;

б) средняя гармоническая величина;

в) средняя геометрическая величина;

г) средняя квадратическая, кубическая и т.д. величины.

3. По охвату совокупности:

а) групповая средняя величина;

б) общая средняя величина.

Средние величины различаются в зависимости от учета признаков, влияющих на осредняемую величину:

Если средняя величина рассчитывается для признака, без учета влияния на него каких-либо других признаков, то такая средняя величина называется простой средней.

Если имеются сведения о влиянии на осредняемый признак некоторого признака или нескольких признаков, которые необходимо учесть при расчете для корректного расчета средней величины, то рассчитывается средняя взвешенная.

По форме расчета выделяют несколько видов средних величин, которые образованы из единой степенной средней величины. Степенная простая средняя величина имеет форму:

где, - среднее значение исследуемого явления;

– сумма отдельных варьирующих вариантов явлений статистической совокупности,

k – показатель степени средней;

– количество варьирующих вариантов явлений статистической совокупности.

Степенная взвешенная средняя величина имеет форму:

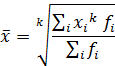
где, – сумма отдельных варьирующих вариантов явлений статистической совокупности,

– количество варьирующих вариантов явлений статистической совокупности,

– частота, или статистический вес, варианта.

При разных показателях степени k получаем, соответственно, различные по форме средние величины.

Таблица 3.1.2

Дата добавления: 2015-03-31