Средние величины

Виды средних	Показатель степени в формуле степенной средней	Формулы средних
простых	взвешенных
Гармоническая	–1
Геометрическая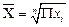
Арифметическая	+1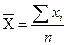
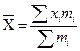
Квадратическая	+2
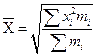
Кубическая	+3
Степенная	Z

Выбор формы средней обусловлен исходным соотношением, суть которого приводилась выше. Существует порядок расчета средней величины:

1. Определение исходного соотношения для исследуемого показателя.

2.Определение недостающих данных для расчета исходного соотношения.

3. Расчет средней величины.

Для каждого из представленных средних показателей кроме последних разработано обоснование его применения, которое увязывается с характером исследуемого статистического массива данных. Проблема использования тех или иных средних показателей состоит в адекватности получаемых результатов реальности изучаемого явления.

Средняя гармоническая используется в случаях, когда вес признака является произведением значений на число единиц, или значение есть отношение веса к числу единиц. В случае изучения подобной совокупности у исследователя появляется необходимость корректировки средней величины в сторону понижения ввиду значимости того факта, что число единиц для каждой исследуемой средней различно.

Средняя геометрическая также используется исследователями в случае необходимости корректировки среднего значения в сторону понижения, в частности, когда даны максимальное и минимальное значение признака, или изучается изменение величины в динамике.

Средняя арифметическая используется в случае, когда средняя изучаемой совокупности не требует корректировки в силу того, что необходимо учесть все причинные факторы влияющее на средний показатель. Это иллюстрируется таким свойством средней величины, которое гласит, что при изменении значений признака на одно и то же число средняя также изменяется на одно и то же число.

Средние более высоких степеней используются при необходимости корректировки среднего показателя в большую сторону относительно средней арифметической в зависимости от характеристик изучаемой совокупности, и факторов, которые лежат в основе значений рассматриваемого признака.

Средняя арифметическая – одна из наиболее распространенных форм средней величины. Средняя арифметическая рассчитывается как частное от деления суммы индивидуальных значений (вариантов) варьирующего признака на их число. Средняя арифметическая применяется в тех случаях, когда объем варьирующего признака явлений однородной статистической совокупности, образуется путем суммирования значений признака всех единиц явлений статистической совокупности. Определяется при подстановке в формулу степенной средней значения k= 1.

Свойства средней арифметической:

1. Сумма отклонений различных значений признака от средней арифметической равна нулю:

2. Если от каждого варианта вычесть или к каждому варианту прибавить какое-либо произвольное постоянное число, то средняя увеличится или уменьшится на то же самое число.

3. Если каждый вариант умножить (разделить) на какое-либо произвольное постоянное число, то средняя увеличится (уменьшится) во столько же раз.

4. Если веса, или частоты, разделить или умножить на какое-либо произвольное постоянное число, то величина средней не изменится.

5. Сумма квадратов отклонений значений признака от средней меньше суммы квадратов отклонений от любой произвольной величины.

6. Произведение средней на сумму частот всегда равна сумме произведений вариантов на частоты.

Расчет средней гармонической производится в случаях, когда известны значения признаков, а вес дан в виде произведения значений признака на число единиц. Определяется при подстановке в формулу степенной средней значения k= -1

Средняя геометрическая величина используется при анализе динамики (для определения среднего темпа роста), и при заданном минимальном и максимальном значении признака. Определяется при подстановке в формулу степенной средней значения k= 0.

Средняя квадратическая величина применяется при расчете показателей вариации и при определении средней длины квадратного участка. Определяется при подстановке в формулу степенной средней значения k= 2.

Средняя кубическая величина используется при расчете осредняемого признака в пространстве.

Средняя должна исчисляться не просто тогда, когда есть вариация признака, а тогда, когда мы располагаем качественно однородным вариационным рядом. Среднюю как обобщающую характеристику нельзя применять к таким совокупностям, отдельные части которых подчиняются различным законам распределения (или) развития в отношении величины распределяемого признака.

Средняя величина, рассчитанная по совокупности в целом, называется общей средней. Она дополняется средними, если совокупность разделить на отдельные группы. Такие средние величины называются групповыми средними.

Дата добавления: 2015-03-31