Понятие и необходимость статистического изучения вариации признака. Показатели вариации, порядок их расчета

Вариация – это изменение (колеблемость) значений признака в пределах изучаемой совокупности при переходе от одного объекта к группе объектов, от одного случая к другому. Абсолютные и относительные показатели вариации позволяют определить степень связи между признаками, оценить степень однородности совокупности, типичности и устойчивости средней, определить величину погрешности выборочного наблюдения, статистически оценить закон распределения совокупности и т.д.

Вариация признака характеризуется: рассеянностью, колеблемостью, индивид значением признака относит средн величины.

Рассмотрим способы расчета показателей вариации.

Размах вариации (R) представляет собой разность между макс (Xmax) и минимум (Xmin) значениями признака в совокупности: R=Xmax-Xmin. Достоинство R – простота расчета. Недостаток – характеризует отклонение крайних значений, но н показывает распределение отклонений внутри совокупности.

Мерой др показателей вариации является разность не между крайними значениями признака, а средняя разность между каждым значением признака и его средней величиной. Разность между отдельным значением признака и средней называют отклонением. Среднее линейное отклонение вычисляется по след формулам:

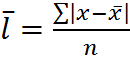простая; 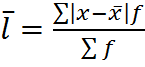взвешенная.

Среднее линейное отклонение имеет ту же размеренность, что и признак, для которого оно исчисляется. Недостаток – не характеризует направление отклонений.

Среднее линейное отклонение относительно редко применяется для оценки вариации признака. Поэтому обычно вычисляется дисперсия (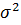) и среднее квадратическое отклонение (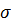). Эти показатели применяются не только для оценки вариации признака, но и для изменения связи между ними, оценки величины ошибки выборочного наблюдения и других целей. Дисперсия - средний квадрат отклонений индивидуальных значений признака от их средней величины.

Дисперсия признака рассчитывается:

Простая 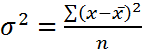; взвешенная .

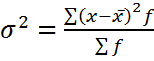Недостаток – не имеет единицы измерения.

Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии. Имеет единицу измерения ту же что и варианты, показывает направление отклонения.

Коэффициент вариации (он равен выраженному в % отношению среднего квадратического отклонения к средней арифметической.

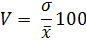
Если коэффициент вариации не превышает 33%, принято считать совокупность качественно однородной.

Такой показатель можно использовать для сравнения размеров вариации разнородных признаков. Коэффициент вариации также используется для сравнения размеров вариации в совокупностях, отличающихся друг от друга величиной средней.

Дата добавления: 2015-03-29