Виды дисперсий и правило их сложения

Дисперсия альтернативного признака (вывод формулы).

Альтернативным называется признак, в котором одни единицы обладают, а другие не обладают. Вариация альтернативного признака у единиц, которые им обладают, количественно проявляется в значении единицы. У тех единиц совокупности, которые не обладают признаком, вариация проявляется в значении нуля. Доля единиц, обладающих признаком, обозначается р. Доля единиц, не обладающая признаком – q.

p+q=1

x	f
	p
	q

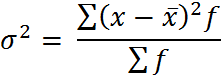
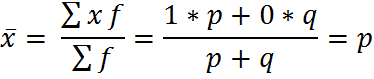
Средняя альтернативная признака всегда равна его доле

(1-p=q)

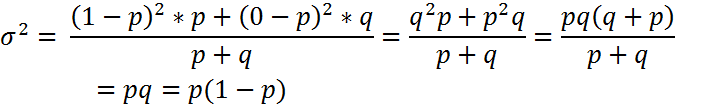
Дисперсия альтернативного признака равно произведению доли на дополнительные доли к единице.

Для оценки влияния различных факторов, определяющих колеблемость индивидуальных значений признака, раскладывают общую дисперсию на составляющие. Если статистическая совокупность разбита на группы по конкретному признаку, то средняя величина и дисперсия признака может определятся не только для всей совокупности, но и для отдельных групп, на которые разбита совокупность. В этом случае возникают групповые и межгрупповые виды вариаций.

Вариацию признака, обусловленную влиянием фактора, положенного в основу группировки, характеризует межгрупповая дисперсия, которая является мерой колеблемости групповых средних вокруг общей средней

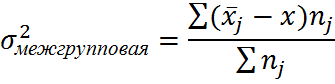
- число единиц совокупности в j-той группе

j- порядковый номер группы

Для характеристики вариации признака, обусловленного влиянием всех факторов кроме группировочного, характеризует внутригрупповая дисперсия

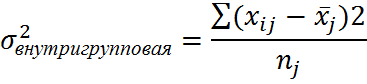
i - порядковый номер группы

Правило сложения дисперсий.

Существует правило сложения дисперсии, в соответствии с которым общая дисперсия определяется как сумма из внутригрупповых и межгрупповых дисперсий:

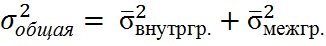
Данное соотношение называют правилом сложения дисперсий. Согласно этому правилу, общая дисперсия, возникающая под действием всех факторов, равна сумме дисперсии, возникающей за счет группировочного признака.

Зная любые два вида дисперсий, можно определить или проверить правильность расчета третьего вида.

Правило сложения дисперсий широко применяется при исчислении показателей тесноты связей, в дисперсионном анализе, при оценке точности типической выборки и в ряде других случаев.

36. Использование правила сложения дисперсий в анализе связей. Расчет показателей оценки тесноты связи.

Существует закон согласно которому, общая дисперсия, возникающая под воздействием всех факторов, равна сумме дисперсии, возникающей за счет группировочного признака и дисперсии, появляющейся под влиянием всех прочих факторов. Этот закон связывает три вида дисперсии.

Правило сложения дисперсий: .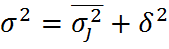

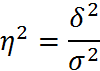Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий. Внутригрупповые дисперсии показывают вариации выработ­ки в каждой группе, вызванные всеми возможными фактора­ми (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), кроме различий в квалификационном разряд. Средняя из внутригрупповых дисперсий отражает вариацию выработки, обусловленную всеми факторами, кроме квалифика­ции рабочих, но в среднем по всей совокупности. Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квали­фикационному разряду. Общая дисперсия отражает суммарное влияние всех возможных факторов на общую вариацию среднечасовой выработки изделий всеми рабочими цеха.Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации (ή ²) — показатель, пред­ставляющий собой долю межгрупповой дисперсии в общей дис­персии результативного признака и характеризующий силу влия­ния группировочного признака на образование общей вариации: Эмпирический коэффициент детерминации показывает долю вариации результативного признака у под влиянием факторного признака х (остальная часть общей вариации у обуславливается вариацией прочих факторов). При отсутствии связи эмпирический коэф равен 0, а при функциональной связи – единице. Эмпирическое корреляционное отношение — это корень квад­ратный из эмпирического коэффициента детерминации: 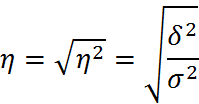Оно показывает тесноту связи между группировочным и результативным признаками.Эмпирическое корреляционное отношение ή, как и ή ², может принимать значения от 0 до 1. Если связь отсутствует, то корреляционное отношение равно нулю, т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет. Значит, группировочный при­знак никак не влияет на образование общей вариации. Если связь функциональная, то корреляционное отношение будет равно единице. В этом случае дисперсия групповых средних равна общей дисперсии, т.е. внутригрупповой вариации не будет. Это означает, что группировочный признак целиком оп­ределяет вариацию изучаемого результативного признака. Чем значение корреляционного отношения ближе к еди­нице, тем теснее, ближе к функциональной зависимости связь между признаками.

Дата добавления: 2015-03-29