
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Способы распространения результатов выборочного наблюдения на генеральную совокупность. Практика применения выборочных исследований в статистике
|
|
|
|
Определение необходимой численности (объема) выборки.
Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц.
Уменьшение стандартной ошибки выборки всегда связано с увеличением объема выборки. Для случайного повторного объема выборки (n) имеем:
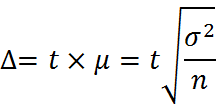
откуда
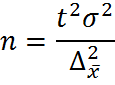
При случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия и дисперсии вариационного признака и обратно пропорционален квадрату предельной ошибки выборки. В частности, с увеличением предельной ошибки в 2 раза необходимая численность выборки может быть уменьшена в 4 раза. Из трех параметров два (коэффициент доверия и предельная ошибка выборке) задаются исследователем. При этом исследователь исходя из цели и задач выборочного обследования должен решить вопрос, в каком количественном сочетании лучше включить эти параметры для обеспечения оптимального варианта. В одном случае его может устраивать в большей мере надежность полученных результатов (t), нежели мера точности (Д), в другом – наоборот. Сложнее решить вопрос в отношении величины предельной ошибки выборки, так как этим показателем исследователь на стадии проектировки выборочного наблюдения не располагает. В практике принято задавать величину предельной ошибки выборки в пределах до 10% предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по-разному: использовать данные подобных ранее проведенных об–следований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку.
При проектировании выборочного наблюдения предполагаются заранее заданная величина допустимой ошибки выборки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения.
В целом формула предельной ошибки выборочной средней позволяет решать следующие задачи:
1) определять величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности;
2) определять необходимую численность выборки, обеспечивающую требуемую точность, при которой пределы возможной ошибки не превысят некоторой, наперед заданной величины;
3) определять вероятность того, что в проведенной выборке ошибка будет иметь заданный предел.
Оценка статистических параметров генеральной совокупности, или распространение (экстраполяция) результатов выборки на генеральную совокупность, осуществляется с учетом ошибки выборки стандартной или предельной) и указанием доверительной вероятности. Чаще всего оцениваются 4 параметра генеральной совокупности:
1) Среднее значение 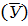
2) Суммарное значение 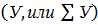
3) Отношение двух суммарных или средних значений 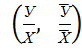
4) Доля единиц, обладающих определенным признаком 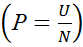
Выделяются простые (прямые) и сложные виды оценок.
Простая оценка представляет собой процесс оценивания простых функций совокупности, таких как среднее, суммарное значение признака, доля единиц. Перечисленные параметры и их оценки тесно взаимосвязаны, являются несмещенными.
Для простого случайного бесповторного и расслоенного отбора оценки основных параметров генеральной совокупности имеют следующий вид:
| Бесповторный случайный отбор | Расслоенный отбор | |
| 1.Оценка суммарного значения | 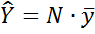
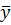 – выборочная средняя – выборочная средняя
| 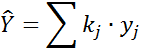
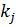 -коэффициент распространения -коэффициент распространения
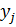 -суммарное значение признака -суммарное значение признака
|
| 2.Оценка численности единиц в генеральной совокупности | 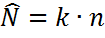 или или
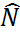 = = 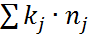
| |
| 3.Оценка среднего значения | 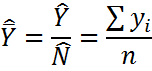
| 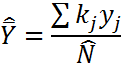
|
| 4.Оценка доли | 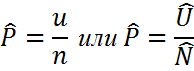 u-число единиц с данным признаком в выборке
U-число единиц с данным признаком в генеральной совокупности
u-число единиц с данным признаком в выборке
U-число единиц с данным признаком в генеральной совокупности
|
Сложные оценки предусматривают совместное оценивание двух характеристик х и у, которыми обладает каждый из N элементов генеральной совокупности. Наиболее часто используются 3 вида сложных оценок: по отношению, регрессии, взвешивание.
По отношению: находятся оценки суммарных значений двух количественных переменных для исходной совокупности, их соотношение выступает искомой величиной.
По регрессии: предполагает оценивание среднего изменения значения у при изменении на единицу значения х.
По взвешиванию: Дополнительная информация привлекается для расчета весов (wi), которые присваиваются каждой обследуемой единице.
| Для среднего значения | Для суммарного значения | ||
| По отношению | Несмещенная оценка | 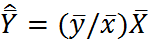
| 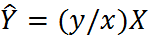
|
| Раздельная оценка | 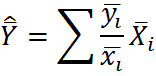
| 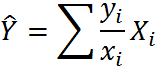
| |
| Совместная оценка | 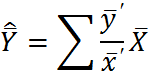
| 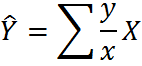
| |
| Регрессии | 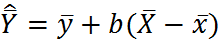
| 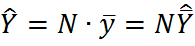
| |
| Взвешиванию | 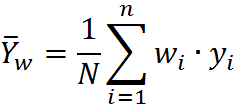
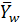 -взвешенное среднее значение по выборке -взвешенное среднее значение по выборке
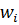 -выборочный вес -выборочный вес
|
|
|
|
|
|
Дата добавления: 2015-03-29; Просмотров: 1138; Нарушение авторских прав?; Мы поможем в написании вашей работы!