Средние индексы и их виды, порядок вычисления

Второй формой сводного индекса являются средние индексы. Различают средний арифметический и средний гармонический формы индексов. Средний арифметический индекс является формой алгебраического преобразования агрегатных факторных индексов объемных показателей. Рассмотрим, как производится преобразование агрегатного индекса физического объема в индекс среднеарифметический. В качестве исходной формы общего индекса возьмем агрегатный индекс физического объема продукции:

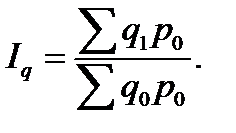
Для преобразования используем значение индивидуального индекса объема продукции 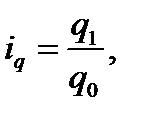из которого следует, что q₁=i_qq₀. Воспользуемся этим равенством и в числителе агрегатного индекса заменим q₁ через i_qq₀. Знаменатель индекса оставим без изменения. Тогда формула индекса физического объема продукции примет такой вид: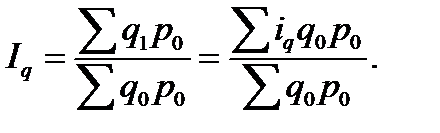

В таком виде индекс физического объема продукции выступает как среднеарифметическая величина из индивидуальных индексов, взвешенных по стоимости продукции базисного периода (q₀p₀). Только при этой системе весов средний арифметический индекс продукции будет тождественен исходному агрегатному индексу и даст количественно тот же результат.

Агрегатный индекс может быть преобразован не только в средней арифметической, но и в средний гармонический. Эта форма индекса получается в результате алгебраического преобразования агрегатных факторных индексов качественных показателей. В этом случае необходимо, допустим, иметь данные об индивидуальных индексах цен

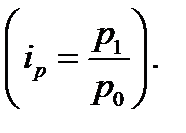
Из формулы расчета индивидуального индекса цен узнаем, чему равняется цена базисного периода: 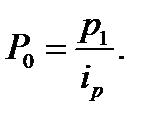Воспользуемся этим равенством и в знаменателе агрегатного индекса цен заменим Р₀ через 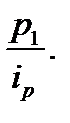Числитель индекса оставим без изменения. Тогда формула индекса цен примет такой вид: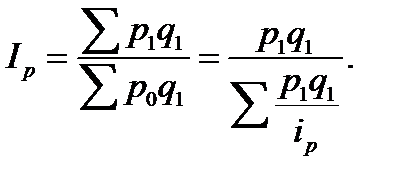

Выведенная формула индекса цен выступает как средняя гармоническая величина из индивидуальных индексов цен, взвешенная по величине фактического товарооборота отчетного периода (p₁q₁). По такой системе весов средний гармонический индекс будет тождественен агрегатному индексу. Применение других систем весов здесь неприемлемо, так как в этих случаях не получим количественный результат, аналогичный агрегатному факторному индексу качественного показателя (цен, себестоимости, урожайности и т.д.).

Так, 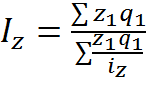средний гармонический индекс себестоимости.

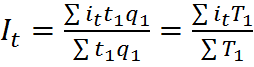- средний арифметический индекс производительности труда.

Дата добавления: 2015-03-29