Понятие прямолинейной корреляции. Нахождение параметров уравнения регрессии, оценка тесноты связи при прямолинейной зависимости

Корреляция – это статистическая зависимость между случайными величинами, не имеющими строго функционального характера, при которой изменение одной из случайных величин приводит к изменению математического ожидания другой.

Первоначально исследования корреляции проводились в биологии, а позднее распространились и на другие области, в том числе на социально-экономическую. Одновременно с корреляцией начала использоваться и регрессия. Корреляция и регрессия тесно связаны между собой: корреляция оценивает силу (тесноту) статистической связи, регрессия исследует ее форму. Та и другая служат для установления соотношения между явлениями, для определения наличия или отсутствия связи.

Корреляционный и регрессионный анализ как общее понятие включает в себя измерение тесноты, направления связи и установление аналитического выражения (формы) связи (регрессионный анализ).

Уравнение регрессии имеет следующий вид:

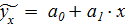, где 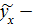выравненные значения результативного признака

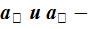параметры уравнения прямой

Если 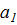> 0, то связь между признаками прямая; 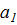< 0- обратная

Конечной целью корреляционного анализа всегда является получение количественной оценки тесноты связи между признаками. Для решения этой задачи используются относительные показатели измерения тесноты связи. К ним относятся коэффициент корреляционного отношения (индекс корреляции) и парный линейный коэффициент корреляции Пирсона :

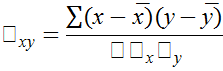
Коэффициент корреляционного отношения применяется для изменения тесноты связи при любых формах зависимости, в то время как парный линейный коэффициент корреляции - только для линейной связи между признаками. При линейной связи значение индекса корреляции и коэффициента корреляции совпадают и показатель тесноты целесообразно исчислять в виде коэффициента корреляции, который представляет собой среднюю арифметическую из произведения нормированных отклонений, т.е.

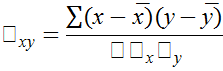
По исходным данным коэффициент корреляции можно исчислять так:

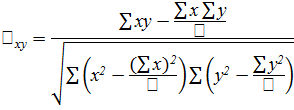
Парный линейный коэффициент корреляции принимает значения от -1 до +1. Если он положительный, то связь между признаками прямая, если отрицательный – обратная.

Дата добавления: 2015-03-29