Понятие криволинейной зависимости. Оценка тесноты связи при криволинейной зависимости

Когда с изменением факторного признака меняется не только признак-результат, но и интенсивность этого изменения, то имеет место нелинейная зависимость.

Для оценки параметров нелинейных уравнений регрессии используется 2 подхода:

· при помощи математических преобразований исходных переменных представляют зависимость в линейной форме

· применяют методы нелинейной оптимизации к исходным данным в том случае, когда линеаризующее преобразование невозможно.

Регрессионное уравнение может быть нелинейным по переменным и нелинейным по параметрам. Если уравнение нелинейно по переменным, то его можно свести к линейному виду путем введения новых переменных.

Примерами регрессионных уравнений, нелинейных по факторным переменным и линейных по оцениваемым параметрам, могут служить:

· уравнение равносторонней гиперболы

· уравнение параболы

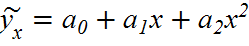
Примерами регрессионных уравнений, линейных по факторным переменным и нелинейных по оцениваемым параметрам, могут служить:

· степенная функция

· экспонента

· показательная функция

62. Понятие о множественной корреляции

При анализе сложных экономич. явлений и процессов всегда следует исходить из предположения, что на анализируемый результативный признак воздействует множество факторов как в одном, так и в противоположных направлениях.

В ходе множественного корреляционного анализа рассчитываются следующие характеристики:

· парные коэффициенты корреляции оценки тесноты линейной корреляционной связи между всеми парами анализируемых признаков с учетом их взаимного влияния и взаимодействия.

· частные коэффициенты корреляции характеризующие тесноту линейной корреляционной связи между парой анализируемых признаков (х_i и у) в условиях элиминирования (элиминирование - это исключение из рассмотрения в процессе анализа, расчета, контроля признаков, факторов, показателей, заведомо не связанных с изучаемым, анализируемым, контролируемым процессом, явлением) влияния на эту пару других переменных(. Эти коэффициенты характеризуют чистую корреляцию.

· множественный коэффициент корреляции характеризующий степень тесноты связи между результативным признаком у и всеми факторными признаками . Для двух факторов, влияющих на результативный признак, множественный коэффициент корреляции вычисляется из парных коэффициентов корреляции по формуле

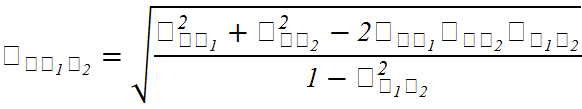
· множественный коэффициент детерминации характеризующий долю дисперсии результативной переменной, обусловленную влиянием факторных переменных, участвующих в анализе.

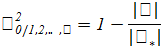
где 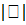- определитель матрицы парных корреляций

- определитель матрицы, полученный после вычеркивания в матрице парных корреляций строки и столбца, представляющих связи зависимой переменной (у).

При множественной корреляционной связи между результативными и факторными признаками чаще всего используется линейная регрессионная модель вида

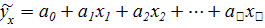
где - значение результативного признака у отдельных единиц совокупности

- перечень признаков-факторов включенных в регрессионное уравнение

а₀ - свободный член уравнения

- коэффициенты регрессии, показывающие на сколько увеличится или уменьшится результативный признак при изменении каждого из признаков-факторов на единицу своего измерения.

Дата добавления: 2015-03-29