Территориальные индексы

Индексный метод может быть использован для исследования различных экономический явлений не только в динамике, но и для пространственных сравнений за один и тот же период по экономическим районам, городам, областям, государствам. В таких случаях прибегают к построению территориальных индексов, которые бывают:

· индивидуальными – представляют собой обычные относительные величины сравнений, и их расчет не вызывает особых затруднений.

Например: в районе А урожайность картофеля составила 232 ц/га, а в районе В-200 ц/га, то индивидуальный территориальный индекс равен

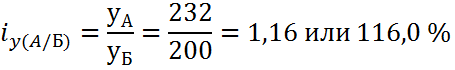
Этот индекс показывает, что в районе А урожайность картофеля в 1,16 раза выше, чем в районе Б.

· общими – их сложнее построить и используют тогда, когда возникает необходимость пространственных по сложным совокупностям, содержащим определенный индексный набор элементов. Разработка методов построения общих территориальных индексов относится к числу важных научно-методологических и практических проблем статистики. Трудность заключается:

ü в выборе базы сравнения (в отличии от динамических индексов, где индексируемая величина отчетного периода сравнивается с базисным, следуя хронологии происходящих явлений, то при построении территориальных индексов нет никакого основания и смысла отдавать предпочтение одной пространственной единицы другой)

ü в выборе весов сравнения (возникает вопрос-количество производимых товаров какого района следует принять в качестве весов). В соответствии с методологическим принципом построения динамических индексов, согласно которому веса качественных индексируемых величин берутся на уровне отчетного периода, можно построить 2 территориальных индекса цен:

1)

2)

где - агрегатный индекс цен, в котором в качестве базы сравнения применяются цены на продукцию района Б, а в качестве весов берутся объёмы продукции произведенной в районе А и наоборот.

Нет никаких оснований для выбора какой-то одной из приведенных выше формул, каждая из них может быть использована с равным правом. Но иногда сделав расчеты по этим формулам можно получить не только различные, а иногда и противоречивые результаты.

Предполагаются различные методы построения общих территориальных индексов.

Так, при построении агрегатных территориальных индексов качественных показателей в качестве весов используют стандартизированные веса.

При построении агрегатных территориальных индексов количественных показателей в качестве соизмерителей в зависимости от целей анализа берутся соответствующие средние показатели отдельных элементов, исчисленные либо по обеим сравниваемым территориям, либо по более широкой территории.

Кроме прямых методов, используется косвенный метод который основывается на использование стандартных значений индексируемых величин.

При этом методе формулы для расчета территориальных индексов качественных показателей имеет вид:

и наоборот;

p_ст. – стандартное значение цен

территориальных индексов количественных показателей:

и наоборот;

Q- стандартное значение количественных характеристик

58. Измерение связей между социально-экономическими явлениями – важнейшая задача статистики. Формы и виды взаимосвязей.

Одна из важнейших задач статистики состоит в том, чтобы изучать связи и зависимости между соц.-экономич. явлениями и процессами. При этом статистическому изучению и измерению подвергаются как полные (функциональные), так и неполные (корреляционные) связи.

Функциональной связью называют такую связь, при которой значения одного признака полностью определяются значениями другого признака.

Признаки по характеру их роли во взаимосвязи подразделяют на факторные (х) (признаки, обуславливающие изменение других, связанных с ними признаков) и результативные (у) (признаки, изменяющиеся под действием факторных).

При функциональной связи каждому значению факторного признака х соответствует одно или несколько определенных значений результативного признака у.

При корреляционной связи нет такого строгого соответствия между значениями факторного и результативного признаков. Каждому значению факторного признака хсоответствует целый ряд значений результативного признака у. Корреляционная связь в отличие от функциональной проявляется не в каждом конкретном случае, а только в среднем при изучении некоторой статистической совокупности явлений. В качестве примера корреляционной зависимости можно привести зависимость между стажем работы и средней заработной платой работающих. Для того, чтобы выявить и измерить такую зависимость, нужно пронаблюдать большое число единиц совокупности.

При исследовании корреляционных связей решаются 2 задачи: выявляется наличие связи между признаками, измеряется ее теснота, выбирается уравнение связи, оцениваются его параметры.

По направлению выделят связь прямую и обратную. Прямая – такая связь, при которой оба вида признаков изменяются в одном и том же направлении. В случае же обратной связи значения результативных признаков изменяются под действием факторных, но в противоположном направлении по сравнению с изменением факторных признаков.

По аналитическому выражению прямолинейные и нелинейные связи. Если статистическая связь явлений может быть приближенно выражена математическим уравнением прямой линии, то ее называют прямолинейной, или линейной связью, если же она может быть выражена уравнением кривой линии (параболы, гиперболы и т.д.), то – нелинейной, или криволинейной.

59. Статистические методы изучения связей: метод сравнения параллельных рядов, метод аналитических группировок, графический метод, балансовый метод.

Для выявления связи, ее характера, направления в статистике используют следующие методы:

· Метод приведения параллельных данных состоит в следующем: приводятся два ряда данных о двух явлениях или двух признаках, связь между которыми необходимо выявить; по характеру изменений делают заключения о наличии (если изменение величин одного ряда следует за изменением величин другого) или об отсутствии связи (если никакого твердого, устойчивого соответствия в их изменении нет);

· Балансовый – заключается в построении балансов-таблиц, в которых итог одной части равен итогу другой (например, баланс производства сахара и его потребления);

· Метод аналитических группировок используется при установлении и изучении причинно-следственных связей между факторными и результативными признаками, т.е. как в массовых явлениях с изменением одного или нескольких факторных признаков изменяются результативные признаки.

· Графический – заключается в следующем. Характер зависимости между двумя признаками можно наглядно увидеть, если построить график, отложив на оси абсцисс ранжированные (возрастающие) значения признака-фактора (х), на оси ординат значения результативного признака (у). Нанеся на график точки, соответствующие значениям х и у, получим корреляционное поле, где и по характеру их расположения можно судить о направлении и силе связи.

ü Если точки беспорядочно разбросаны по всему полю, то это указывает на то, что зависимости между двумя признаками нет;

ü если они будут концентрироваться вокруг оси, идущей от нижнего левого угла в верхний правый, то имеется прямая зависимость между варьирующими признаками;

ü если точки будут концентрироваться вокруг оси, идущей от верхнего левого угла в нижний правый, то имеется обратная зависимость.

Дата добавления: 2015-03-29