Контрольная работа № 5

.

Учтя, что λ<< b_mах и что членом, содержащим λ², можно пренеб­речь, последнее равенство перепишем в виде

r² =2λ b_max. откуда b_max =r²/(2λ). Произведя вычисления по последней формуле, найдем

b_max=1 м.

Пример 4. На щель шириной а =0,1 мм нормально падает параллельный пучок света от монохроматического источника (λ==0,6 мкм). Определить ширину l центрального максимума в дифракционной картине, проецируемой с помощью линзы, нахо­дящейся непосредственно за щелью, на экран, отстоящий от лин­зы на расстоянии L =l м.

Решение. Центральный максимум интенсивности света за­нимает область между ближайшими от него справа и слева миниму­мами интенсивности. Поэтому ширину центрального максимума интенсивности примем равной расстоянию между этими двумя минимумами интенсивности (рис. 5).

Минимумы интенсивности света при дифракции от одной щели наблюдаются под углами φ, определяемыми условием

a sin φ=± k λ, (1)

где k — порядок минимума; в нашем случае равен единице.

Расстояние между двумя минимумами на экране определим не­посредственно по чертежу: l=2L tgφ. Заметив, что при малых уг­лах tg φ sin φ, перепишем эту формулу в виде

Рис. 5

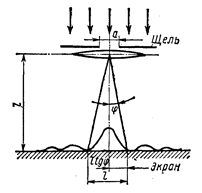l =2L sin φ. (2)

Выразим sin φ из формулы (1) и подставим его в равенство (2):

l=2Lkλ/a. (3)

Произведя вычисления по фор­муле (3), получим l =1,2 см.

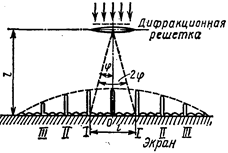
Пример 5. На дифракционную решетку нормально к ее поверх­ности падает параллельный пучок света с длиной волны λ=0,5мкм. Помещенная вблизи решетки лин­за проецирует дифракционную картину на плоский экран, удаленный от линзы на L =l м. Расстоя­ние l между двумя максимумами интенсивности первого порядка, наблюдаемыми на экране, равно 20,2 см (рис. 6). Определить: 1) постоянную d дифракционной решетки; 2) число n штрихов на 1 см; 3) число максимумов, которое при этом дает дифракционная решетка; 4) максимальный угол φ _mах отклонения лучей, соот­ветствующих последнему дифракционному максимуму.

Решение 1. Постоянная d дифракционной решетки, длина волны λ и угол φ отклоне­ния лучей, соответствую­щий k-му дифракционному максимуму, связаны соот­ношением

dsin φ= k λ, (1)

где k — порядок спектра, или в случае монохрома­тического света порядок максимума.

В данном случае k =1, sin φ=tg φ (ввиду того, что l /2<< L), tgφ=(l /2) L (следует из рис. 31.3). С учетом последних трех равенств соотношение (1) примет вид

Рис. 6 ,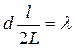

откуда постоянная решетки

d =2 L λ/ l.

Подставляя данные, получим

d =4,95 мкм.

2. Число штрихов на 1 см найдем из формулы

п =1/ d.

После подстановки числовых значений получим n =2,02-10³ см^-1.

3. Для определения числа максимумов, даваемых дифракцион­ной решеткой, вычислим сначала максимальное значение k_max исходя из того, что максимальный угол отклонения лучей решеткой не может превышать 90°.

Из формулы (1) запишем

. (2)

Подставляя сюда значения величин, получим

K_max =9,9.

Число k обязательно должно быть целым. В то же время оно не может принять значение, равное 10, так как при этом значении sin φ должен быть больше единицы, что невозможно. Следователь­но, k_mах =9.

Определим общее число максимумов дифракционной картины, полученной посредством дифракционной решетки. Влево и вправо от центрального максимума будет наблюдаться по одинаковому числу максимумов, равному k_mах, т. е. всего 2 k_mах. Если учесть также центральный нулевой максимум, получим общее число мак­симумов

N =2 k_max +l.

Подставляя значение k_mах найдем

N =2∙9+1=19.

4. Для определения максимального угла отклонения лучей, соответствующего последнему дифракционному максимуму, выра­зим из соотношения (2) синус этого угла:

sinφ_max= k_max λ/ d.

Отсюда

φ_max=arcsin(k_max λ/ d).

Подставив сюда значения величин λ, d, k_mах и произведя вычис­ления, получим

φ _mах =65,4°.

Пример 6. Исследование спектра излучения Солнца показы­вает, что максимум спектральной плотности энергетической све­тимости соответствует длине волны λ=500 нм Принимая Солнце за черное тело, определить. 1) энергетическую светимость Me Солнца;

2) поток энергии Ф_е, излучаемый Солнцем; 3) массу т электромаг­нитных волн (всех длин), излучаемых Солнцем за 1 с.

Решение: 1. Энергетическая светимость M_e черного тела выражается формулой Стефана — Больцмана

R_e=sT⁴ (1)

Температура излучающей поверхности может быть определена из закона смещения Вина. λ_m=b/T. Выразив отсюда температуру Т и подставив ее в формулу (1), получим

R_e=s (bλ_m)⁴, (2)

Произведя вычисления по формуле (2), найдем

R_e =64 МВт/м².

2. Поток энергии Ф_е, излучаемый Солнцем, равен произведению энергетической светимости Солнца на площадь S его поверхности.

Ф_е = 4πr²R_e, (3)

где r — радиус Солнца

Подставив в формулу (3) значения π, r и R_e и произведя вычис­ления, получим

Ф_е =3,9∙10²⁶ Вт.

3. Массу электромагнитных волн (всех длин), излучаемых Солн­цем за время t=1 с, определим, применив закон пропорциональ­ности массы и энергии Е=тс². Энергия электромагнитных волн, излучаемых за время t, равна произведению потока энергии Ф (мощ­ности излучения) на время Е=Фt. Следовательно, Ф_е = тс², откуда т= Ф_е /с²

Произведя вычисления по этой формуле, найдем

m = 4,3∙10⁹ кг.

Пример 7. Длина волны λ_m, на которую приходится максимум энергии в спектре излучения черного тела, равна 0,58 мкм. Опре­делить максимальную спектральную плотность энергетической светимости (r_λ,T)_max, рассчитанную на интервал длин волн ∆λ=1нм, вблизи λ_m.

Решение. Максимальная спектральная плотность энергети­ческой светимости пропорциональна пятой степени температуры Кельвина и выражается формулой

(r_λ,T)_max = СТ⁵. (1)

Температуру Т выразим из закона смещения Вина λ_m =b/Т, откуда Т=b/λ_т

Подставив полученное выражение температуры в формулу (1), найдем

(r_λ,T)_max=C(b/λ_m)⁵,

В табл. 24 значение С дано в единицах СИ, в которых единичный интервал длин волн ∆λ=1 м. По условию же задачи требуется вы­числить спектральную плотность энергетической светимости, рас­считанную на интервал длин волн 1 нм, поэтому выпишем значение С в единицах СИ и пересчитаем его на заданный интервал длин волн:

С=1,30∙10^-5 Вт/(м³К⁵)=1,30∙10^-5 Вт/(м²∙м∙K⁵) =

=1,30∙10^-14 Вт/(м²∙нм∙К⁵).

Вычисление по формуле (2) дает

(r_λ,T)_max=40,6 кВт/(м∙нм).

Пример 8. Определить максимальную скорость v_max фотоэлект­ронов, вырываемых с поверхности серебра: 1) ультрафиолетовым излучением с длиной волны λ₁ =0,155 мкм; 2) γ-излучением с длиной волны λ₂=2,47 пм.

Решение. Максимальную скорость фотоэлектронов опреде­лим из уравнения Эйнштейна для фотоэффекта:

ε =A+T_max (1)

Энергия фотона вычисляется по формуле ε = hc/λ, работа выхода для серебра A =4,7 эВ.

Кинетическая энергия фотоэлектрона в зависимости от того, ка­кая скорость ему сообщается, может быть выражена или по класси­ческой формуле

T= ½ m₀v² (2)

или по релятивистской

Т = (m—m₀)c² (3)

Скорость фотоэлектрона зависит от энергии фотона, вызывающе­го фотоэффект: если энергия фотона ε много меньше энергии покоя электрона Е₀ , то может быть применена формула (2); если же ε сравнима по размеру с Е₀ , то вычисление по формуле (2) приводит к грубой ошибке, в этом случае кинетическую энергию фотоэлектрона необходимо выражать по формуле (3)

1. В формулу энергии фотона ε = hc/λ подставим значения вели­чин h, с и λ и, произведя вычисления, для ультрафиолетового излу­чения получим

ε₁ = 8 эВ.

Это значение энергии фотона много меньше энергии покоя элек­трона (0,51 МэВ). Следовательно, для данного случая максимальная кинетическая энергия фотоэлектрона в формуле (1) может быть вы­ражена

по классической формуле (2) ε₁=A+ ½ m₀v²_max, откуда

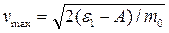(4)

Выпишем величины, входящие в формулу (4): ε₁=1,28×10^-18 Дж (вычислено выше); A=4,7 эВ = 4,7×1,6∙10^-19 Дж = 0,75∙10^-18 Дж; m₀=9,11×10^{-31 кг}.

Подставив числовые значения в формулу (4), найдем максималь­ную скорость:

v_max =1,08 Мм/с.

2. Вычислим теперь энергию фотона γ-излучения:

ε₂=hc/λ₂ = 8,04 фДж = 0,502 МэВ.

Работа выхода электрона (A = 4,7 эВ) пренебрежимо мала по сравнению с энергией γ-фотона, поэтому можно принять, что макси­мальная кинетическая энергия электрона равна энергии фотона:

T_max = ε₂=0,502 МэВ.

Так как в данном случае кинетическая энергия электрона сравни­ма с его энергией покоя, то для вычисления скорости электрона следует взять релятивистскую формулу кинетической энергии,

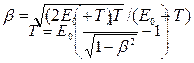где E₀=m₀c².

Выполнив преобразования, найдем

Сделав вычисления, получим

β = 0,755.

Следовательно, максимальная скорость фотоэлектронов, вырывае­мых γ-излучением,

v_max=cβ=226 Mм/c.

Пример 9. Определить красную границу λ₀ фотоэффекта для цезия, если при облучении его поверхности фиолетовым светом длиной волны λ=400 нм максимальная скорость v_max фотоэлектро­нов равна 0,65 Мм/с.

Решение. При облучении светом, длина волны λ₀ которого соответствует красной границе фотоэффекта, скорость, а следова­тельно, и кинетическая энергия фотоэлектронов равны нулю. Поэтому уравнение Эйнштейна для фотоэффекта ε =A+T в случае красной границы запишется в виде

ε = A, или hc/ λ₀ =A.

Отсюда

λ₀ =hc/A. (1)

Работу выхода для цезия определим с помощью уравнения Эйн­штейна:

(2)

Выпишем числовые значения величин, выразив их в СИ: h=6,62∙10^-34 Дж∙с; с = 3∙10⁸ м/с; λ=400 нм=4∙10^{-7 м;} m=9,11∙10^{-31 кг;} v = 6,5∙10⁵ м/с.

Подставив эти значения величин в формулу (2) и вычислив, полу­чим

A=3,05×10^-19 Дж = 1,9 эВ.

Для определения красной границы фотоэффекта подставим значения A, h и с в формулу (1) и вычислим:

λ₀=651 нм.

Пример 10. Пучок монохроматического света с длиной волны λ = 663 нм падает нормально на зеркальную плоскую поверхность Поток энергии Ф_е=0,6 Вт. Определить силу F давления, испытывае­мую этой поверхностью, а также число N фотонов, падающих на нее за время t=5 с

Решение Сила светового давления на поверхность равна произведению светового давления р на площадь S поверхности:

F=pS. (1)

Световое давление может быть найдено по формуле

P=E_e(ρ+l)/c. (2)

Подставляя выражение (2) дaвлeния света в формулу (1), получим

F= [(E_eS)/c]∙(ρ+1). (3)

Так как произведение облученности E_e на площадь S поверх­ности равно потоку Ф энергии излучения, падающего на поверх­ность, то соотношение (3) можно записать в виде

F = (Ф_е/с)∙(ρ+1).

После подстановки значений Ф_е и с с учетом, что ρ=1 (поверх­ность зеркальная), получим

F==4 нН.

Число N фотонов, падающих за время ∆t на поверхность, опре­деляется по формуле

N=∆W/ε = Ф_е ∆t/ε,

где ∆W — энергия излучения, получаемая поверхностью за время ∆t

Выразив в этой формуле энергию фотона через длину волны (ε =hc/λ), получим

N= Ф_еλ∆t/(hc).

Подставив в этой формуле числовые значения величин, найдем

N= 10¹⁹ фотонов.

Пример 11. Параллельный пучок света длиной волны λ=500 нм падает нормально на зачерненную поверхность, производя давление p=10 мкПа. Определить: 1) концентрацию п фотонов в пучке, 2) число n₁ фотонов, падающих на поверхность площадью 1 м² за вре­мя 1 с.

Решение. 1. Концентрация п фотонов в пучке может быть найдена, как частное от деления объемной плотности энергии w на энергию ε одного фотона:

n=w/ε (1)

Из формулы p=w(1+ρ), определяющей давление света, где ρ-коэффициент отражения, найдем

w = p/(ρ+1). (2)

Подставив выражение для w из уравнения (2) в формулу (1), получим

n = ρ/[(ρ+1)∙ε]. (3)

Энергия фотона зависит от частоты υ, а следовательно, и от длины световой волны λ:

ε = hυ = hc/λ (4)

Подставив выражение для энергии фотона в формулу (3), опре­делим искомую концентрацию фотонов:

n = (ρλ)/[(ρ+1)∙ε]. (5)

Коэффициент отражения ρ для зачерненной поверхности прини­маем равным нулю.

Подставив числовые значения в формулу (5), получим

n=2,52∙10¹³ м^-3.

2. Число n₁ фотонов, падающих на поверхность площадью 1 м² за время 1 с, найдем из соотношения n₁=N/(St), где N — число фо­тонов, падающих за время t на поверхность площадью S. Но N=ncSt, следовательно,

n₁=(ncSt)/(St)=nc

Подставив сюда значения п и с, получим

n₁=7,56∙10²¹ м^-2∙с^-1.

Пример 12. В результате эффекта Комптона фотон при соударе­нии с электроном был рассеян на угол θ=90°. Энергия ε ' рассеянного фотона равна 0,4 МэВ. Определить энергию ε фотона до рассеяния.

Решение. Для определения первичного фотона воспользу­емся формулой Комптона в виде

λ`-λ = 2×[(2πħ)/(mc)]×sin²(θ/2). (1)

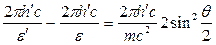Формулу (1) преобразуем следующим образом: 1) выразим длины волн λ' и λ через энергии ε' и ε соответствующих фотонов, восполь­зовавшись соотношением ε = 2πħc/λ; 2) умножим числитель и зна­менатель правой части формулы на с. Тогда получим

Сократив на 2nħc, выразим из этой формулы искомую энергию:

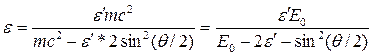
ε = 1,85 МэВ.

Пример 13. Фотон с энергией ε =0,75 МэВ рассеялся на свобод­ном электроне под углом θ=60°. Принимая, что кинетическая энер­гия и импульс электрона до соударения с фотоном были пренебре­жимо малы, определить: 1) энергию ε' рассеянного фотона; 2) кинетическую энергию Т электрона отдачи; 3) направление его движения.

Решение. 1. Энергию рассеянного фотона найдем, восполь­зовавшись формулой Комптона:

Выразив длины волн λ' и λ через энергии ε' и ε соответствующих фотонов, получим

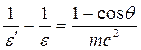
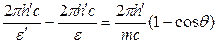
(1)

Разделим обе части этого равенства на 2πħc:

От­сюда, обозначив для краткости энергию покоя электрона тc² через е_о, найдем

Подставив числовые значения величин, получим

ε'=0,43 МэВ.

2. Кинетическая энергия электрона отдачи, как это следует из закона сохранения энергии, равна разности между энергией ε па­дающего фотона и энергией е' рассеянного фотона:

T = ε - ε` = 0,32 МэВ.

3. Направление движения электрона отдачи найдем, применив закон сохранения импульса, согласно которому импульс падающего фотона р равен векторной сумме импульсов рассеянного фотона р' и электрона отдачи mv:

p = p'+mv.

Векторная диаграмма импульсов изображена на рис.. Все векторы проведены из точки О, где находился электрон в момент соударения с фотоном. Угол φ определяет направление движения электрона отдачи.

Из треугольника OCD находим

или

Так как р=ε/с и р'=е'/с, то

(2)

Рис. 7

Преобразуем формулу (2) так, чтобы угол φ выражался непосредственно через величины ε и θ, за­данные в условии задачи. Отсюда

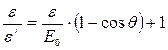(3)

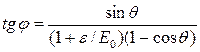Заменим в формуле (2) соотношение ε/ε' по формуле (3):

Учитывая, что sin θ=2sin(θ/2)cos(θ/2) и 1—cosθ=2sin²(θ/2), после соответствующих преобразований получим

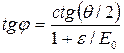(4)

После вычисления по формуле (4) найдем tg φ =0,701, откуда φ=35°.

Пример 14. Вычислить радиус первой орбиты атома водорода (Боровский радиус) и скорость электрона на этой орбите.

Решение. Согласно теории Бора, радиус r электронной ор­биты и скорость v электрона на ней связаны равенством тvr=пħ. Так как в задаче требуется определить величины, относящиеся к первой орбите, то главное квантовое число n=1 и указанное выше равенство примет вид

mvr=ħ. (1)

Для определения двух неизвестных величин r и v необходимо еще одно уравнение. В качестве второго уравнения воспользуемся уравнением движения электрона. Согласно теории Бора, электрон вращается вокруг ядра. При этом сила взаимодействия между электрическими зарядами ядра и электрона сообщает электрону центростремительное ускорение. На основании второго закона Нью­тона можем записать

(е и m — заряд и масса электрона), или

(2)

Совместное решение равенств (1) и (2) относительно r дает

r = 4πε₀ ħ/(me²).

Подставив сюда значения ħ, е, т и произведя вычисления, най­дем боровский радиус:

r = а = 5,29∙10^{-11 м.}

Из равенства (1) получим выражение скорости электрона на первой орбите:

υ= ħ /(mr).

Произведя вычисления по этой формуле, найдем

υ = 2,18 Мм/с.

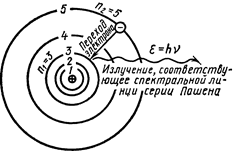
Пример 15. Определить энергию ε фотона, соответствующего вто­рой линии в первой инфракрасной серии (серии Пашена) атома водорода.

Решение. Энергия ε фотона, излучаемого атомом водорода при переходе электрона с одной орбиты на другую,

Рис.8

где E_i — энергия иониза­ции атома водорода; m=1,2,3,...—номер орбиты, на которую переходит электрон (рис. 8); n=m+1;

m+2;... — номер орбиты, с которой переходит электрон. Для серии Пашена m=3; для второй линии этой серии n= 3+2=5.

Подставив числовые значения, найдем энергию фотона:

ε = 0,97 эВ.

Пример 16. Электрон, начальной скоростью которого можно пренебречь, прошел ускоряющую разность потенциалов U. Найти длину волны де Бройля l для двух случаев: 1) U ₁= = 51 кВ; 2) U ₂= 510 кВ.

Решение. Длина волны де Бройля l частицы зависит от ее импульса р и определяется формулой

l = 2 pħ/p (1)

Импульс частицы можно определить, если известна ее кинетичес­кая энергия Т. Связь импульса с кинетической энергией для не­релятивистского (когда T << E ₀) и для релятивистского (когда T» E ₀ ) случаев соответственно выражается формулами:

; (2)

(3)

Формула (1) с учетом соотношений (2) и (3) запишется соответ­ственно в нерелятивистском и релятивистском случаях:

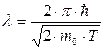; (4)

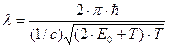(5)

Сравним кинетические энергии электрона, прошедшего заданные в условии задачи разности потенциалов U ₁ = 51 В и U ₂ = 510 кВ, с энергией покоя электрона и в зависимости от этого решим вопрос, которую из формул (4) и (5) следует применить для вычисления длины волны де Бройля.

Как известно, кинетическая энергия электрона, прошедшего ус­коряющую разность потенциалов U,

T = | e | U.

В первом случае T ₁ = | e |(U ₁ = 51 эВ = 0,51×10^-4 МэВ, что много меньше энергии покоя электрона E ₀ = m ₀ c² = 0,51 МэВ. Следователь­но, можно применить формулу (4).

Для упрощения расчетов заметим, что T₁ = 10^-4 m ⁰ c ². Подставив это выражение в формулу (4), перепишем ее в виде

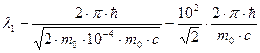
Учтя, что 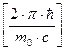есть комптоновская длина волны l_C, получим .

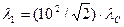Так как l_C = 2,43×10^{-12 м} , то

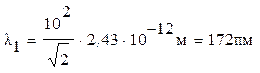
Во втором случае кинетическая энергия Т ₂= ½е½ U ₂ = 510 кэВ = 0,51 МэВ, т. е. равна энергии покоя электрона. Следовательно, необходимо применить релятивистскую формулу (5).

Учтя, что Т₂ =0,51 МэВ=mc², по формуле (5) найдем

Подставив значение l_с в последнюю формулу и произведя вы­числения, получим

l₂=1,4 пм.

Пример 17. На узкую щель шириной а = 1 мкм направлен парал­лельный пучок электронов, имеющих скорость = 3,65 Мм/с. Учи­тывая волновые свойства электронов, определить расстояние х между двумя максимумами интенсивности первого порядка в дифракционной картине, полученной на экране, отстоящем на L = 10 см от щели.

Решение. Согласно гипотезе де Бройля, длина волны l, соответствующая частице массой т, движущейся со скоростью, выражается формулой

l = 2pħ/(mu). (1)

Дифракционный максимум при дифракции на одной щели наб­людается при условии

a sin j = (2 k +1)(l/2), (2)

где k = 0, 1, 2, 3,...—порядко­вый номер максимумов; a — ши­рина щели.

Для максимумов первого порядка (k =1) угол j заведомо мал, по­этому sin j = j, и, следовательно, формула (2) примет вид

aj = ³/₂l, (3)

а искомая величина х, как следует из рис. 9,

x = 2L tg j = 2Lj, (4)

так как tg j = j.

Получим

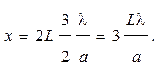
Подстановка в последнее равенство длины волны де Бройля по формуле (1) дает

.

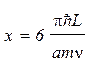После вычисления по формуле (5) получим

x = 6 · 10-41=60 мкм.

Пример 18. На грань кристалла никеля падает параллельный пучок электронов. Кристалл поворачивают так, что угол скольже­ния θ изменяется. Когда этот угол делается равным 64°, наблюдается максимальное отражение электронов, соответствующее дифракцион­ному максимуму первого порядка. Принимая расстояние d между атомными плоскостями кристалла равным 200 пм, определить длину волны де Бройля λ электронов и их скорость ν.

Решение. К расчету дифракции электронов от кристалли­ческой решетки применяется то же уравнение Вульфа — Брэгга, которое используется в случае рентгеновского излучения:

2d sin θ = kλ

где d — расстояние между атомными плоскостями кристалла: θ — угол скольжения; k — порядковый номер дифракционного макси­мума; λ — длина волны де Бройля. Очевидно, что

λ = (2 d sin θ)/k.

Подставив в эту формулу значения величин и вычислив, получим

λ =360 пм.

Из формулы длины волны де Бройля λ = 2πħ/(mν) выразим ско­рость электрона:

ν = 2πħ/(mλ)

Подставив в эту формулу значения π, ħ, m (масса электрона), и произведя вычисления, найдем

v=2 Мм/с.

Пример 19. Кинетическая энергия Т электрона в атоме водорода составляет величину порядка 10 эВ. Используя соотношение неопре­деленностей, оценить минимальные линейные размеры атома.

Решение. Неопределенность координаты и импульса элект­рона связаны соотношением

ΔxΔp ≥ ħ (1)

где Δ x — неопределенность координаты электрона; Δ р — неопреде­ленность его импульса.

Из этого соотношения следует, что чем точнее определяется положение частицы в пространстве, тем более неопределенным становится импульс, а следовательно, и энергия частицы. Пусть атом имеет линейные размеры l, тогда электрон атома будет находиться где-то в пределах области с неопределенностью: Δ x = l /2. Соотноше­ние неопределенностей (1) можно записать в этом случае в виде (l/2} Δ p ≥ ħ, откуда

l ≥ 2 ħ /(Δ р) (2)

Физически разумная неопределенность импульса Δ p, во всяком случае, не должна превышать значения самого импульса р, т. е.

Δ p ≤ p

Импульс р связан с кинетической энергией Т соотношением Заменим Δ p значением (такая замена не увеличит l). Переходя от неравенства (2) к равенству, получим

l_min = 2ħ/

Подставив числовые значения и произведя вычисления, найдем l_min = 124 пм.

Пример 20. Используя соотношение неопределенностей энергии и времени, определить естественную ширину ∆λ спектральной линии излучения атома при переходе его из воз­бужденного состояния в основное. Сред­нее время τ жизни атома в возбужденном состоянии принять равным 10^-8 с, а дли­ну волны λ излучения равной 600 нм.

Рис. 10

Решение. При переходе атомов из возбужденного состояния в основное су­ществует некоторый разброс (неопреде­ленность) в энергии испускаемых фотонов. Это связано с тем, что энергия возбужден­ного состояния не является точно апре­ль деленной, а имеет конечную ширину Г (рис. 10). Согласно со­отношению неопределенностей энергии и времени, ширина Г энер­гетического уровня возбужденного состояния связана со средним временем т жизни атомов в этом состоянии соотношением

Г_τ ~ ħ

Тогда ширина энергетического уровня определяется выражением

Г = ħ / τ

Вследствие конечной ширины уровня энергии возбужденного состоя­ния энергия фотонов, испускаемых атомами, также имеет разброс, равный ширине энергетического уровня, т. е. ∆ε = Г.

Тогда

∆ε = ħ/ τ (1)

Поскольку энергия е фотона связана с длиной волны λ соотношением

ε = 2πħc/λ

то разбросу ∆ε (∆ε << ε) энергии соответствует разброс ∆λ длин волн (∆λ<<λ)

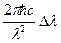
∆ε = (2)

(знак минус опущен).

Входящий в это выражение конечный интервал длин волн Д?.и есть естественная ширина спектральной линии. Выразив Д^ из фор­мулы (2) и заменив Де согласно (1), получим

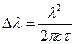
Произведем вычисления:

∆ λ = 2 · 10^-14м =20 фм

Пример 21. Определить начальную активность А₀ радиоактив­ного магния 27Mg массой m=0,2 мкг, а также активность А по исте­чении времени t=1 ч. Предполагается, что все атомы изотопа ра­диоактивны.

Решение. Начальная активность изотопа

А₀ = λN₀ (1)

где λ — постоянная радиоактивного распада; N₀ — количество ато­мов изотопа в начальный момент (t=0).

Если учесть, что

то формула (1) примет вид

Выразим входящие в эту формулу величины в СИ и произведем вычисления:

A₀=5,15×10¹² Бк=5,15ТБк.

Активность изотопа уменьшается со временем по закону

A=A₀ e^-λt (3)

Заменив в формуле (3) постоянную распада λ ее выражением, по­лучим

A=A₀ e^-ln2*t/T1/2 =A₀ (e^ln2)^-t/T1/2

Так как e^ln2 = 2 окончательно будем иметь

A=A₀ /2^t/T1/2

Сделав подстановку числовых значений, получим A=8,05×10¹⁰ Бк= 80,5 ГБк.

Пример 22. При определении периода полураспада T_1/2 короткоживущего радиоактивного изотопа использован счетчик импульсов. За время ∆t = 1 мин в начале наблюдения (t=0) было насчитано ∆n₁=250 импульсов, а по истечении времени t=1 ч - ∆n₂=92 импуль­са. Определить постоянную радиоактивного распада λ и период полураспада T_1/2 изотопа.

Решение. Число импульсов ∆n, регистрируемых счетчиком за время ∆t, пропорционально числу распавшихся атомов ∆N.

Таким образом, при первом измерении

∆n₁=k∆N₁=kN₁(1-e^–λ∆t), (1)

где N₁ — количество радиоактивных атомов к моменту начала от­счета; k — коэффициент пропорциональности (постоянный для данного прибора и данного расположения прибора относительно радиоактивного изотопа).

При повторном измерении (предполагается, что расположение приборов осталось прежним)

∆n₂=k∆N₂=kN₂(1-e^–λ∆t), (2)

где N₂ — количество радиоактивных атомов к моменту начала вто­рого измерения.

Разделив соотношение (1) на выражение (2) и приняв во внима­ние, что по условию задачи ∆t одинаково в обоих случаях, а также что N₁ и N₂. связаны между собой соотношением N₂ = N₁ e^-λt, по­лучим

∆n₁/∆n₂=e^λt (3)

где t — время, прошедшее от первого до второго измерения. Для вы­числения l выражение (3) следует прологарифмировать: In(∆n₁/∆n₂)=λt, откуда

λ = (1/t)×ln(∆n₁/∆n₂).

Подставив числовые данные, получим постоянную радиоактив­ного распада, а затем и период полураcпада:

λ = (1/1)×ln(250/92)ч^-1 = 1ч^-1;

T_1/2 = ln2/λ = 0,693/1 = 0,693ч = 41,5 мин.

Таблица вариантов

Вариант	Номера задач

Дата добавления: 2015-03-31