Явления переноса

Молекулярно-кинетическая теория

· Концентрация частиц (молекул, атомов и т. п.) однородной системы

n=N /V,

где V — объем системы.

· Основное уравнение кинетической теории газов

p=²/зn< e_п >,

где р — давление газа; <e_п>— средняя кинетическая энергия* поступательного движения молекулы.

· Средняя кинетическая энергия:

приходящаяся на одну степень свободы молекулы

<e₁>=½k T;

;

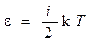поступательного движения молекулы

,

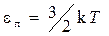где k — постоянная Больцмана; Т — термодинамическая темпера­тура; i — число степеней свободы молекулы;

вращательного движения молекулы

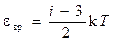
· Зависимость давления газа от концентрации молекул и тем­пературы

p = n k T.

· Скорость молекул:

средняя квадратичная

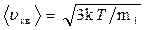, или ;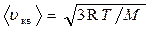

средняя арифметическая

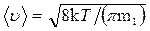, или ;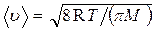

наиболее вероятная

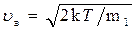, или ,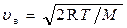

где m₁ — масса одной молекулы.

· Среднее число соударений, испытываемых одной молекулой газа в единицу времени,

,

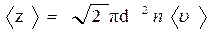где d — эффективный диаметр молекулы; п — концентрация моле­кул; <υ> — средняя арифметическая скорость молекул.

· Средняя длина свободного пробега молекул газа

.

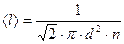· Импульс (количество движения), переносимый молекулами из одного слоя газа в другой через элемент поверхности,

,

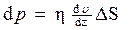где h— динамическая вязкость газа; 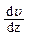—градиент (поперечный) скорости течения его слоев; DS — площадь элемента поверхности; d t — время переноса.

· Динамическая вязкость

h= 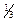r<υ>< l >

где r — плотность газа (жидкости); < υ > — средняя скорость хаоти­ческого движения его молекул; < l > — их средняя длина свободного пробега.

· Закон Ньютона

,

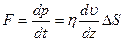где F — сила внутреннего трения между движущимися слоями газа.

· Закон Фурье

DQ= -l 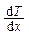SDt,

где DQ — теплота, прошедшая посредством теплопроводности через сечение площадью S за время Dt; l — теплопроводность; 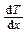-градиент температуры.

· Теплопроводность.(коэффициент теплопроводности) газа

l= 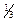c_vr<υ>< l > или l= 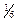<υ>< l >,

где c_v — удельная теплоемкость газа при постоянном объеме; r — плотность газа; <υ> — средняя арифметическая скорость его молеку­лы; < l > — средняя длина свободного пробега молекул.

· Закон Фика

,

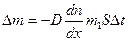где Dm — масса газа, перенесенная в результате диффузии через поверхность площадью S за время Dt; D — диффузия (коэффициент Эффузии); 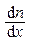- градиент концентрации молекул; m₁ — масса одной молекулы.

· Диффузия (коэффициент диффузии)

D= 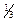<υ>< l >.

Статистические распределения

· Распределение Больцмана (распределение частиц в силовом поле)

n=n ₀e^{-U/(k T)},

где п — концентрация частиц; U — их потенциальная энергия; n ₀ — концентрация частиц в точках поля, где U=0; k — постоян­ная Больцмана; T — термодинамическая температура.

· Барометрическая формула (распределение давления в одно­родном поле силы тяжести)

р=p ₀e^{-mgz/(k T )}, или p=p ₀e ^{-M gz/(R T)},

где р — давление газа; m — масса частицы; М — молярная масса; z — координата (высота) точки по отношению к уровню, принятому за нулевой; р ₀ — давление на этом уровне; g — ускорение свобод­ного падения; R — молярная газовая постоянная.

· Вероятность того, что физическая величина х, характери­зующая молекулу, лежит в интервале значений от х до x +d x, определяется по формуле

d W(x)=f(x) d x

где f(x) —функция распределения молекул по значениям данной физической величины х (плотность вероятности).

· Количество молекул, для которых физическая величина х, характеризующая их, заключена в интервале значений от х до x +d x,

d N=N d W(x)=Nf(x) d x.

· Распределение Максвелла (распределение молекул по ско­ростям) выражается двумя соотношениями:

а) число молекул, скорости которых заключены в пределах от J до J+dJ,

,

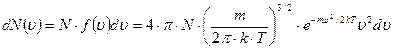где f (υ) — функция распределения молекул по модулям скоростей, выражающая отношение вероятности того, что скорость молекулы лежит в интервале от υ до υ+dυ, к величине этого интервала, а также долю числа молекул, скорости которых лежат в указанном интервале; N — общее число молекул; m — масса молекулы;

б) число молекул, относительные скорости которых заключены в пределах от u до u +d u,

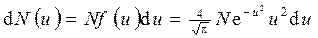
где u =υ/υ_в — относительная скорость, равная отношению скорости J к наивероятнейшей скорости υ_в; f (u) — функция распределения по относительным скоростям.

· Распределение молекул по импульсам. Число молекул, им­пульсы которых заключены в пределах от р до p +d p,

,

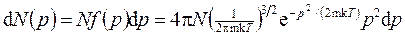где f (p) — функция распределения по импульсам.

· Распределение молекул по энергиям. Число молекул, энер­гии которых заключены в интервале от e до e+de,

,

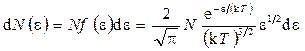где f (e)—функция распределения по энергиям.

· Среднее значение физической величины х в общем случае

,

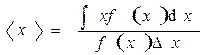а в том случае, если функция распределения нормирована на еди­ницу,

< x> =ò xf (x)d x

где f(x) — функция распределения, интегрирование ведется по всей совокупности изменений величины х.

Например, среднее значение скорости молекулы (т. е. средняя арифметическая скорость)

;

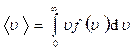средняя квадратичная скорость

<υ_кв>=<υ²>^1/2,

где

;

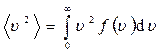средняя кинетическая энергия поступательного движения молекулы .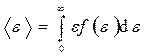

Дата добавления: 2015-03-31