Тема № 3 Механические колебания и волны

Колебаниями называется процесс, в котором значения какой-либо физической величины повторяются точно или приблизительно точно через равные или приблизительно равные промежутки времени. Такое движение играет важную роль в самых разнообразных вопросах физики. Важнейшим среди колебательных движений является так называемое гармоническое колебательное движение. Аналитически гармонические колебания описываются формулой

x = A cos(ωt + φ₀). (3.1)

В этой формуле х – смещение изменяющейся величины от положения равновксия; А – амплитуда колебаний, которая равна максимальному смещению; ω – циклическая частота; а аргумент косинуса называют фазой колебаний, φ₀ – начальной фазой. Время одного полного колебания называется периодом колебаний Т. Число колебаний, совершаемых за единицу времени, называется частотой колебаний ν. Очевидно, что ω = 2πν; а также Т = 1/ν = 2π/ω.

Продифференцируем выражение (3.10) два раза по времени:

= ̶ ω² A cos(ωt + φ₀) = ̶ ω² x.

Таким образом, уравнение (3.1) является одним из решений дифференциального уравнения:

+ ω² x = 0. (3.2)

Рассмотрим колебания твердого тела относительно неподвижной горизонтальной оси (Рис.3.1).

На рисунке ось вращения обозначена буквой О, С-центр масс

О тела. Положение тела можно характеризовать углом отклоне-

а α ния его от положения равновесия α. Основно уравнение дина-

С. С₁ мики вращательного движения в рассматриваемом случае

имеет вид:

I = ̶ mga sin α (3.3)

где I – момент инерции тела относительно оси О, а – расстоя-

Рис. 3.1 ние от оси вращения до центра масс, m – масса тела.

Для малых отклонений можно принять sin α = α и формула (3.3) принимает вид:

+ mga α/I = 0. (3.4)

При сравнении формул (3.4) и (3.2) видно, что малые колебания нашего тела (физического маятника) будут гармоническими с циклической частотой

ω =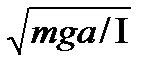

и периодом

Т = 2π 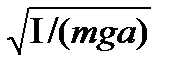(3.5)

Частным случаем физического маятника является математический маятник. Примером математического маятника может служить шарик, подвешенный на длинной нити длиной l.

В этом случае а = l. I = ml² и формула (3.5) переходит в

Т = 2π (3.6)

Напомним без вывода формулу для периода колебаний груза массой m на пружине жёсткостью k из курса физики средней школы

Т = 2π 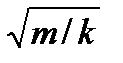(3.7)

Процесс распространения колебаний (возмущений) в пространстве, несущий с собой энергию, называют волной. Волны бывают продольными и поперечными. В продольной волне частицы среды, создающие волну, совершают колебания в направлении распространения волны. В поперечной волне частицы среды смещаются перпендикулярно к направлению распространения волны. Смещение точек одномерной волны, распространяющейся вдоль оси х, обычно описывают уравнением:

у = А cos (ωt kx + φ₀), (3.8)

где k – волновое число. Аргумент косинуса в формуле (3.8) называется, как и в случае колебаний, фазой. Минимальное расстояний между точками волны, совершающими колебания в одинаковой фазе называется длиной волны λ. Если х = λ. то сдвиг фазы равен 2π, поэтому

k = 2π/λ (3.9)

Скорость распространения волны

v = λ/Т = λν (3.10)

Жидкости и газы обладают только объёмной упругостью, поэтому в них могут распространяться только продольные волны.

Дата добавления: 2015-03-31