Тема № 4 Молекулярная физика

4.1 Молекулярно-кинетическая теория

Идея об атомном строении вещества возникла в глубокой древности, однако молекулярно-кинетическая теория (МКТ) в окончательном виде была построена в XIX веке. Обоснованием этой теории послужили закон кратных отношений в химии, работы Авогадро, Ломоносова, Максвелла, Больцмана и др. Убедительным доказательством МКТ является броуновское движение открытое английским ботаником Броуном в 1827 г., которое заключается в том, что все мельчайшие частицы, взвешенные в жидкости, находятся в непрерывном дрожании. Взвешенными называются макроскопические тела, которые падают в вязкой среде со скоростью, практически незаметной для человеческого глаза. Будем считать для простоты, что частица имеет форму шара радиусом а, с плотностью ρ, которая больше плотности среды ρ₀. На неё действуют сила тяжести, сила Архимеда и сила сопротивления среды. Сила тяжести направлена вниз, остальные две силы – вверх. Сумму сил тяжести и Архимеда называют кажущимся весом

P* = mg ̶ ρ₀gm/ρ = mg(1 ̶ ρ₀/ρ) (4.1)

Т.к. сила сопротивления среды зависит от скорости частицы. То через определенный промежуток времени движение частицы становится равномерным. Скорость установившегося движения частицы зависит от её радиуса а. Если считать, что сила сопротивления пропорциональна площади сечения частицы (~ а ²) и её скорости v, а масса пропорциональна а ³. то скорость установившегося движения частицы пропорциональна её радиусу, т.е. чем меньше размеры частицы, тем медленнее она падает.

Броуновское движение никогда не прекращается. Оно было обнаружено в жидких включениях кварца, которым тысячи лет. Интенсивность броуновского движения возрастает при увеличении температуры и уменьшении вязкости жидкости. Теория броуновского движения была разработана в начале ХХ века Эйнштейном и Смолуховским.

Наиболее простым агрегатным состоянием вещества является газообразное. Для описания состояния газа используются такие физические величины, как давление, объём и температура.

Давление в механике определяется как отношение модуля силы, действующей перпендикулярно некоторой площадке к площади S этой площадки:

Р = F_n/S (4.2)

Единицей измерения давления в системе СИ является паскаль (Па). Давление атмосферы было измерено в начале XVII Э. Торричелли по высоте поднятия ртути в вертикальной трубке, введённая тогда единица измерения давления – мм рт. ст. используется и в настоящее время.

1 мм рт. ст. 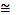133,3 Па (4/3 гПа).

Для выяснения молекулярно- кинетического смысла давления рассмотрим очень упрощенную модель газа. Будем считать, что все молекулы имеют одинаковую скорость v и могут двигаться только вдоль трех координатных осей в положительном и отрицательном направлениях. Кроме этого, будем считать, что молекулы сталкиваются только со стенками сосуда, а друг с другом не сталкиваются. Силы притяжения между молекулами учитывать не будем. В этом приближении в положительном направлении.например, оси Х, перпендикулярной одной из стенок, будет перемещаться 1/6 часть всех молекул. Выделим на этой стенке площадку ΔS, за промежуток времени Δt об эту площадку ударится 1/6 ΔS v Δt n молекул (n-концентрация молекул), каждая из которых сообщит площадке импульс 2 mv (m-масса одной молекулы). Тогда давление равно отношению суммарного импульса, сообщенного площадке ΔS к Δt и ΔS

Р = 1/3 n m v² (4.3)

Т.к. кинетическая энергия одной молекулы ε_к = mv²/2, то формула (4.3) примет вид:

Р = 2/3 n ε_к (4.4)

Соотношение (4.4) называют иногда основным уравнением молекулярно-кинетической теории. Если учесть, что молекулы имеют разные скорости и сталкиваются друг с другом, то получается такая же формула, только под ε_к понимается средняя кинетическая энергия поступательного движения одной молекулы. Это обстоятельство, конечно, не оправдывает простоту рассматриваемой модели газа. Если в этих же предположениях определить число

ударов молекул z об единицу площади стенки в единицу времени, то получится формула

z = 1/6n v (4.5)

В точной формуле, полученной с учётом того, что все молекулы имеют разные скорости и сталкиваются друг с другом, численный множитель равен 1/4.

Выясним теперь молекулярно-кинетический смысл температуры. Для этого умножим (4.4) на объём V:

P V = 2/3 N Е_к (4.6)

Таким образом произведение давления на объём пропорционально средней кинетической энергии поступательного движения молекул газа. С другой стороны. Для идеального газа справедливо уравнение Клапейрона –Менделеева:

Р V = ν RT (4.7)

Сравнивая формулы (4.6) и (4.7) можно сделать однозначный вывод о том, что произведение давления и объёма для данной массы газа определяется с одной стороны температурой газа, а с другой стороны – кинетической энергией поступательного движения молекул, поэтому кинетическую энергию 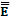_к или любую монотонную функцию её можно принять за меру температуры. попробуем суммировать наши сведения о температуре.

1. Температура –макроскопический параметр, характеризующий термодинамическую систему в состоянии термодинамического равновесия, т. Е. нет смысла спрашивать о температуре одной молекулы или температуре кипятка, в котором плавает кусок льда.

2. С точки зрения МКТ температура характеризует интенсивность теплового движения молекул, например для идеального газа она пропорциональна кинетической энергии поступательного движения молекул.

3. Для количественного измерения температуры используются температурные шкалы. Шкала Цельсия строится по двум реперным точкам – нормальной точке плавления льда и нормальной точке кипения воды. Нормальная точка плавления льда – равновесная температура чистого льда и насыщенной воздухом воды при нормальном давлении (760 мм рт. ст.). Вторая точка – температура кипения воды при нормальном давлении. Первой точке присваивается температура 0 ⁰С, - второй – 100 ⁰С.

Удобно за меру температуры взять величину

Θ = 2/3 _к/N, (4.8)

При этом формула (4.6) принимает вид

PV = N Θ, (4.9)

напоминающий уравнение Клапейрона-Менделеева. Величина Θ называется энергетической температурой и должна измеряться в джоулях, однако о историческим причинам для измерения температуры в термодинамике используется кельвин (К). Отношение Θ/T называется постоянной Больцмана k=1,38 10^‒23 Дж/К. Основное уравнение МКТ теперь принимает вид:

P = n kT (4.10)

4.2 Статистические распределения.

При тепловом движении в состоянии термодинамического равновесия все направления скоростей молекул равновероятны, но модули всех скоростей молекул не могут быть одинаковыми, т.к. молекулы часто сталкиваются друг с другом. Задача о распределении молекул газа по скоростям была решена в 1859 г. Максвеллом. Примем произвольную точку пространства О за начало координат, отложим от неё в некоторый момент времени векторы скоростей всех молекул газа. Концы векторов образуют пространство скоростей. Возьмём в пространстве скоростей малый элемент объёма, имеющий, например, форму прямоугольного параллелепипеда с рёбрами dv_х, dv_у, dv_z и с центром в точке v_х, v_у, v_z. Объём этого параллелепипеда равен dω = dv_х dv_у dv_z, число скоростных точек в нём обозначим через dN. Среднее значение 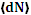зависит от N, dω и от скорости ν, т.е.

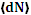= N f(v) dω (4.11)

Величина f(v) называется функцией распределения молекул по скоростям. Если 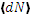проинтегрировать по всему пространству скоростей, то, очевидно, получится полное число молекул N. Отсюда следует условие нормировки. которому должна удовлетворять функция f(v)

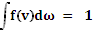(4.12)

Приведём без вывода вид функции распределения, полученный Максвеллом:

f(v) = 4π (m/(2πkT))^3/2 v² exp (‒ mv²/(2kT)) (4.13)

Прямое измерение скоростей молекул в атомном пучке впервые было проведено в 1920 г. О. Штерном в опытах, ставших классическими. Упрощённая схема опыта изображена на рис.4.2.

Платиновая нить А, покрытая серебром, располагалась

вдоль оси цилиндра С. Пространство внутри цилиндра

D₁ откачивалось до давления порядка 10^-5 мм рт. ст. При

С пропускании электрического тока нить А разогрева-

А. D лась, серебро испарялось и его атомы через узкую щель

В В двигались равномерно и прямолинейно к цилиндру С

и при конденсации на его поверхности образовывали

узкую полоску D. При вращении системы с большой

скоростью на цилиндре С появлялось размытое изобра-

Рис.4.2 жение щели D₁, что указывает на то, что атомы серебра

Двигаются с различными скоростями. Полученные при обработке результатов значения скорости в пределах погрешностей совпадали с результатами вычислений по формулам Максвелла.

Pассмотрим идеальный газ в однородном поле тяжести при постоянной температуре.

Рассмотрим вертикально расположенный цилиндрический столб

h газа площадью S. В этом цилиндре выделим объём толщиной dh,

находящийся на высоте h. Для его равновесий необходимо, чтобы

разность давлений снизу и сверху уравновешивала вес газа в выделеном

dh объёме, т.е.

‒ dP S = n mg S dh,

где n – концентрация молекул на высоте h. При постоянной температуре

g S из (4.10) dP = kT dn и после разделения переменных получаем

dn/n = ‒mg dh/kT (4.14)

После интегрирования с начальными условиями n = n₀ при h = 0 получаем:

ln(n/n₀) = ‒ mgh/kT (4.15)

и после потенциирования получаем распределение Больцмана:

n = n₀ exp (‒ mgh/kT) (4.16)

Для изменения давления из (4.16) получаем барометрическую формулу:

P = P₀ exp (‒ Мgh/RT) (4.17)

Применим распределение Больцмана к уединенной планете, окружённой изотермической газовой атмосферой. Потенциальная энергия молекулы с учётом закона всемирного тяготения на расстоянии r равна

Е_п = 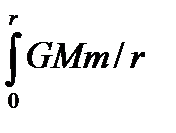²dr =  GMm/r (4.18)

Распределение Больцмана принимает вид

n = n₀ exp (GMm/(rkT)) (4/.19)

Как видно из (4.19) на бесконечном расстоянии от планеты Концентрация не равна нулю. Это является следствием того, что атмосфера не равновесна. Молекулы, имеющие скорости большие второй космической скорости, могут покидать атмосферу. Для массивных планет процесс рассеивания атмосферы происходит крайне медленно В учебнике Д. В. Сивухина подробно исследован этот процесс., в частности там приводятся результаты расчёта температуры газа (К), при которой концентрация молекул различных газов уменьшается в e раз за время τ = 10¹⁰ лет, которое больше чем в 2 раза превышает возраст Земли.

ПЛАНЕТА / ГАЗ	N2	O2	H2	H2O	He
Земля	5 540	6 340		3 560
Луна
Марс	1 130	1 300
Венера	4 690	5 360		3 010
Юпитер	168 000	192 000	12 000	108 000	24 000

Из таблицы видно, что Земля надёжно удерживает в атмосфере все газы, кроме водорода и гелия, а Луна практически лишена атмосферы.

Рассмотрим явления переноса в газах. В эту группу явлений включают внутреннее трение. диффузию и теплопроводность. Объединяет эти явления механизм передачи каких-либо микроскопических характеристик молекул, - через столкновения\ молекул друг с другом. Для количественного описания этих явлений Клаузиус ввёл понятие средней длины свободного пробега, т.е. среднего расстояния, которое пролетает молекула от одного столкновения до следующего. Для упрощения задачи предположим, что движется только одна молекула с постоянной скоростью v, а остальные молекулы неподвижны Назовём эффективным диаметром молекулы d минимальное расстояния между центрами масс сталкивающихся молекул. Вообразим, что с движущейся молекулой жестко связана сфера радиуса d, эта сфера при движении молекулы описывает ломаный цилиндр, очевидно, что движущаяся молекула столкнётся со всеми другими молекулами, центры которых находятся внутри цилиндра. Объём цилиндра за единицу времени равен πd²v. Если концентрация молекул равна n, то в единицу времени произойдёт

z = nπd² v

столкновений, а среднее расстояние между столкновениями равно

λ = 1/n πd² (4.20)

Строгий расчёт, проведённый Максвеллом с учётом распределения молекул по скоростям, даёт

λ = 0,71/n πd² (4.21)

Рассмотрим две параллельные пластинки, между которыми находится газ. Одна из пластин неподвижна, а вторая двигается со скоростью u. Чтобы поддерживать эту скорость постоянной, к движущейся пластинке необходимо прикладывать силу F. Если расстояние между пластинами равно l, а площадь одной пластины – S, то, как это экспериментально установлено Ньютоном,

F = η S u/ll (4.22)

Коэффициент η в этой формуле называется коэффициентом внутреннего трения или вязкостью. Если направить ось х перпендикулярно пластинам, то формулу (4.22) можно записать так

F = η S du/dх (4.23)

Как показала МКТ, вязкость газа связана с микроскопическими величинами, характеризующими движение молекул, формулой

η = 1/3 ρ v λ (4.24)

1Явление теплопроводности описывается экспериментально установленным законом Фурье. Плотность потока тепла пропорциональна в одномерном случае производной температуры по координате

q = ‒ æ dТ/dх, (4.25)

где коэффициент теплопроводности æ выражается через микроскопические величины следующим образом:

æ = 1/3 ρ v λ с_V (4.26)

Диффузией называется проникновение молекул одного газа среди молекул другого газа. Если молекулы обоих газов мало отличаются друг от друга, то диффузию принято называть самодиффузией. Для наблюдения самодиффузии нужно как-то «пометить» часть молекул. Если

Концентрация «меченых» молекул равна n_1, то для одномерной самодиффузии выполняется закон Фика, диффузионный поток (количество «меченных» молекул через единичную площадку в единицу времени) пропорционален производной концентрации по координате

Г₁ = ‒ D dn₁/dх, (4.27)

а коэффициент диффузии

D = 1/3 v λ (4.28)

Расчет взаимной диффузии для газов, молекулы которых сильно отличаются друг от друга, представляет собой непростую задачу.

Дата добавления: 2015-03-31