Тема № 5 Термодинамика

5.1 Первое начало термодинамики

В основе термодинамики лежат так называемые начала, которые являются обобщением большого числа опытов. Термодинамика, в отличии от молекулярной физики, опирается на макроскопические параметры, характеризующие термодинамическую систему в состоянии равновесия. При рассмотрении изменения состояния систем широко используются квазистатические роцессы, состоящие из непрерывно следующих друг за другом состояний равновесия.Такие процессы, строго говоря, никогда не реализуются в природе они являются физическими абстракциями. Однако многие реальные процессы, идущие с конечными скоростями, часто могут считаться приблизительно квазистатическими. В термодинамике часто используются следующие квазистатические процессы: 1) изотермический процесс, происходящий при постоянной температуре (Т = const); 2) изобарический процесс (Р = const); 3) изохорический процесс (V = const).

Рассмотрим газ в цилиндре под поршнем площадью S. Если давление газа равно Р. то при перемещении поршня на расстояния dl совершается элементарная работа δА = РS dl. Поскольку изменение объёма в этом случае равно dV = S dl, то газ совершает работу

δА = Р dV (5.1)

Чтобы от элементарной работы перейти к работе для конечного процесса, надо вычислить интеграл

А = ∫ Р dV

Так как давление зависит не только от объёма, но и от температуры, то работа зависит не только от начального и конечного состояния, но и от пути перехода. Про величины такого рода говорят, что они являются функциями состояния. Из геометрического смысла интеграла следует, что работа численно равна площади фигуры под графиком процесса в переменных V, Р.

Важным понятием термодинамики является адиабатическая оболочка. Состояние системы, заключённой в адиабатическую оболочку, остаётся неизменным при любых изменениях температур окружающих тел, если только значения внешних параметров поддерживаются постоянными. В опытах Джоуля по определению механического эквивалента теплоты было доказано, что работа внешних сил, совершенная над системой, заключенной в адиабатическую оболочку, не зависит от пути перехода системы из начального состояния в конечное.

Внутренней энергией U системы называется функция состояния, приращение которой во всяком процессе, совершаемой системой в адиабатической оболочке, равно работе внешних сил над системой при переводе её из начального состояния в конечное.

Внутренняя энергия идеального одноатомного газа определяется кинетической энергией его молекул. Как следует из формулы (4.8),

U = 3/2 ν RТ (5.2)

Внутреннюю энергию системы можно изменить не только производством работы, но и путём теплообмена. Процесс обмена внутренними энергиями между телами, не сопровождающийся совершением макроскопической работы, называется теплообменом.\Энергия, переданная телу окружающей средой в результате теплообмена, называется количеством тепла.

Сформулируем теперь первое начало термодинамики. Оно утверждает, что теплота Q, полученная системой, идёт на приращение её внутренней энергии и на производство внешней работы

Q = ΔU + А (5.3)

Для элементарных процессов первое начало записывают в виде

δQ = dU + δА (5.4)

Такая запись подчёркивает, что только внутренняя энергия является функцией состояния.

Из первого начала термодинамики следует, что невозможно совершить работу большую, чем полученная теплота, невозможно построить вечный двигатель первого рода, имеющий коэффициент полезного действия, большим единицы.

Теплоёмкостью тела С называется отношение бесконечно малого количества тепла δQ, полученного телом, к соответствующему приращению dТ его температуры:

С = δQ/dТ (5.5)

Особое значение имеют теплоёмкости при постоянном объёме С_V и постоянном давлении С_Р.

При постоянном объёме dV = 0 и

С_V = (∂U/∂Т)_V (5.6)

При постоянном давлении

С_Р = (∂Q/∂Т)_Р (5.7)

Для идельного газа внутренняя энергия зависит только от температуры, поэтому

С_Р = С_V + Р dV/dT,

Тогда

С_Р ‒ С_V = νR (5.8)

Полученная формула называется уравнением Майера.

Получим уравнение адиабатического процесса. Так как δQ = 0, тодля одного моля

С_V dТ + Р dV = 0

.

Из уравнения Клапейрона - Менделеева

dT = (P dV + V dP)/R,

отсюда с учётом уравнения Майера

С_V V dP + C_P P dV = 0

Разделим полученное соотношение на С_P P V и обозначим γ = С_Р/С_V

dP/P + γ dV/V = 0

Отсюда после интегрирования и потенциирования получаем

Р V^γ = const (5.9)

Полученное соотношение называется уравнением Пуассона или уравнением адиабаты, а показатель степени при V в этом уравнении – показателем адиабаты.

Рассмотрим коротко классическую теорию теплоёмкостей идеального газа. В основе этой теории лежит теорема о равномерном распределении энергии по степеням свободы. Число степеней свободы системы i равно минимальному числу независимых координат, необходимых для однозначного описания системы. По этой теореме на каждую степень свободы одной молекулы приходится энергия, равная 1/2 kТ. Тогда внутренняя энергия ν молей идеального газа равна

U = i/2 ν RT, (5.10)

где число степеней свободы равно: 3 для одноатомных молекул, 5 -для двухатомных молекул и 6 – когда i ≥ 3. В этом случае

С_V = i/2 νR; С_Р = (i + 2)/2 νR; γ = (i + 2)/i. (5.11)

Например для воздуха, состоящего в основном из двухатомных молекул, показатель адиабаты при расчётах по формулам (5.11) равен 1,40, а табличное значение при нормальных условиях равно 1.41.

5.2 Второе начало термодинамики

Второе начало термодинамики позволяет судить о направлении процессов, которые могут происходить в системе. Вильям Томсон (лорд Кельвин) дал такую формулировку постулата второго начала термодинамики: «Невозможен круговой процесс, единственным результатом которого быпо бы производство работы за счёт охлаждения теплового резервуара». В такой формулировке второе начало термодинамики отрицает возможность построения вечного двигателя второго рода, имеющего коэффициент полезного действиям η = 1. Клаузиус дал существенно иную формулировку второго начала термодинамики: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому». Несмотря на кажущееся различие, обе формулировки эквивалентны. В термодинамике различают обратимые и необратимые процессы. Если в результате какого-либо процесса система перешла из состояния 1 в состояние 2 и если можно хотя бы одним способом вернуть её в состояние 1 так, чтобы во всех остальных телах не произошло никаких изменений, то процесс называется обратимым. Если же обратный процесс невозможен, переход из 1 в 2 считается необратимым. Анализируя работу тепловых машин в своей знаменитой работе «Размышления о движущей силе огня и машинах, способных развивать эту силу», Сади Карно рассмотрел работу идеальной машины, работающей по знаменитому циклу Карно. Эта машина получает от первого теплового резервуара (нагревателя) количество тепла Q₁ и отдает второму резервуару (холодильнику) количество тепла Q₂, совершая работу А = Q₁ ‒ Q₂. Карно доказал две теоремы: 1) «Коэффициент полезного действия тепловой машины, работающей по циклу Карно, зависит только от температур Т₁ и Т₂ нагревателя и холодильника но не зависит ни то устройства машины, ни от вида используемого рабочего вещества»; 2) «Коэффициент полезного действия всякой тепловой машины не может превосходить к.п.д. идеальной машины, работающей по циклу Карно с теми же самыми температурами нагревателя и холодильника». Обе теоремы Карно можно объединить неравенством

(Q₁ ‒ Q₂)/Q₁ ≤ (T₁ ‒ T₂)/T₁ (5.12)

Для идеальной машины

Q_1//Q₂ = Т₁/Т₂ (5.13)

В 1848 г. Вильямс Томсон (лорд Кельвин) указал, что теоремой Карно можно воспользоваться для построения температурной шкалы, совершенно не зависящей от индивидуальных особенностей термометрического вещества и устройства термометра. Для этого можно приписать какой – либо реперной точке определённое значение температуры, а температуру любого другого тела определить по формуле (5.13). Построенная таким образом шкала называется абсолютной термодинамической шкалой температур. За реперную точку такой шкалы принята тройная точка воды, ей приписано значение температуры 273,16 К точно. Из такого определения температуры следует, что она не может быть отрицательной.

Из неравенства (5.12) следует интересное соотношение

Q₁/Т₁ ‒ Q₂/Т₂≤ 0 (5.14)

Клаузиус обобщил это неравенство на случай произвольного числа тепловых резервуаров. Количество тепла, отданного тепловым резервуаром, считается положительным Отношение Q/Т называется приведённым количеством тепла. Тогда для кругового процесса

∮δQ/Т ≤ 0 (5.15)

Это фундаментальное соотношение называется неравенством Клаузиуса. Если круговой процесс, совершаемый системой, - квазистатический, то неравенство Клаузиуса переходит в равенство

∮ δQ/Т = 0 (5.16)

квст

На этом равенстве основано введение фундаментального в термодинамике понятия энтропии.

Энтропия системы есть функция её состояния, убыль которой равна приведённому количеству тепла, которое необходимо сообщить системе для её перевода из начального состояния 1 в конечное состояние 2 по любому квазистатическому путии Таким образом по определению

S₂ ‒ S₁ = ∫ δQ/Т (5.17)

1→2

Если система переходит из состояния 1 в состояние 2 по любому пути, а возвращается назад по квазистатическому, то из неравенства Клаузиуса получаем

S₂ ‒ S₁ ≥ ∫ δQ/Т.

1→2

Если система адиабатически изолирована, то δQ = 0, тогда

S₂ ≥ S₁. (5.18)

Таким образом, энтропия адиабатически изолированной системы не может убывать. Это – закон возрастания энтропии.

Наряду с энтропией, в термодинамике используются множество других, связанных с ней функций состояния. Особо важное значение имеют две функции: свободная энергия или потенциал Гельмгольца Ψ, и термодинамический потенциал или потенциал Гиббса Ф. Эти функции состояния определяются выражениями

Ψ = U ‒ Т S, (5.19)

Ф = Ψ + Р V. (5.20)

Для их дифференциалов легко получить

dΨ ≤ ‒ S dT ‒ P dV (5.21)

dФ ≤ ‒ S dT + V dP (5.22)

При изотермическом процессе dТ = 0 и dΨ ≤ ‒ δА, т.е. убыль свободной энергии при изотермическом процессе даёт максимальную работу, которую может произвести система.

А убыль термодинамического потенциала даёт максимальную полезную работу, которую может произвести система.

Дальнейшие исследования в этой области привели к появлению важнейшей термодинамической функции – энтропии. Энтропия системы есть функция состояния, определённая с точностью до произвольной постоянной. Разность энтропий в двух равновесных состояниях 2 и 1, по определению, равна приведённому количеству теплоты, которое надо сообщить системе, чтобы перевести её из состояния 1 в состояние 2 по любому квазистатическому пути. S₂ – S₁ = 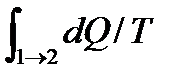. Энтропия адиабатически изолированной системы не может убывать; она либо возрастает, либо остаётся постоянной. Это – закон возрастании энтропии.

Важную роль в природе занимает играет поверхностное натяжение на поверхности жидкости. Силы поверхностного натяжения резко возрастают при увеличении кривизны поверхности жидкости. В тонких цилиндрических капиллярах при наличии смачивания вода может подниматься вверх на высоту в десятки метров.

В учении о фазах выясняются условия, при которых система, состоящая и нескольких фаз, находится в равновесии, а также анализируется влияние различных факторов на фазовые превращения.

5.3 Поверхностное натяжение

На молекулу жидкости действуют силы притяжения со стороны окружающих молекул. Если молекула находится внутри жидкости, эти силы в среднем уравновешиваются, если же она находится вблизи поверхности, то появляется результирующая сила, направленная внутрь жидкости. Поэтому для извлечения молекулы из внутренних частей жидкости на её поверхность требуется затрата работы. Величина, численно равная работе, которую необходимо совершить, чтобы изотермически и квазистатически увеличить поверхность жидкости на единицу при сохранении её объёма неизменным, называется коэффициентом поверхностного натяжения σ жидкости. Изотермическая работа, как известно, равна убыли свободной энергии системы, которую можно представить в виде суммы объёмной и поверхностной составляющих

Ψ = Ψ_об + Ψ_пов (5.23)

Так как объём не изменяется, то

σ = Ψ_пов/F, (5.24)

где F - площадь поверхности жидкости. Таким образом,, коэффициент поверхностного натяжения можно также определить как свободную поверхностную энергию жидкости, приходящуюся на единицу её поверхности.

В состоянии равновесия свободная энергия системы должна быть минимальной, т.к. при постоянных Т и V из (5.21) следует, что dΨ ≤ 0. Поэтому в отсутствии внешних полей жидкость должна принять форму шара, т.к. из всех тел данного объёма шар имеет наименьшую поверхность, а потому и наименьшую свободную энергию. Получению шаровой формы капли мешает сила тяжести.

Принцип минимума свободной поверхностной энергии в применении к растворам приводит к интересному заключению. Состав поверхностного слоя может существенно отличаться от состава основной массы жидкости. Дело в том, что различные чистые вещества имеют разные коэффициенты поверхностного натяжения, поэтому минимум свободной энергии может достигаться путём укомплектования поверхностного слоя такими молекулами, чтобы Ψ была минимальной. Вещества, адсорбирующиеся на поверхности жидкости с понижением σ, называются поверхностно-активными. Наиболее известным примером поверхностно-активного вещества является мыло. Коэффициент поверхностного натяжения жидкости уменьшается также при её нагревании.

Если поместить каплю жидкости на горизонтальную поверхность, то между касательной к поверхностью жидкости и поверхностью твердого тела образуется два угла. Тот угол, который заключает в себе жидкость, называется краевым углом θ. Если краевой угол острый, то говорят, что жидкость смачивает поверхность, если θ – тупой угол, то говорят, что жидкость не смачивает поверхность. Если поверхность жидкости изогнута, то давление по разные стороны её разные. Разность давлений для астигматической поверхности определяется формулой Лапласа

ΔР = σ (1/R₁ + 1/R₂), (5.25)

где R₁и R₂ радиусы кривизны двух взаимно перпендикулярных нормальных сечений поверхности жидкости. Если поверхность жидкости – сферическая, то (5.25) переходит в

ΔР = 2σ/R (5.26)

Внутри мыльного пузыря, оболочка которого имеет две поверхности, разность давлений

ΔР = 4σ/R. (5.27)

Будем считать поверхность жидкости

Применим формулу Лапласа для расчёта высоты h поднятия жидкости в капилляре (от лат. Capillary – волос) радиуса r. Будем считать поверхность жидкости к капилляре сферической с радиусом кривизны R = r/cos θ, где θ – краевой угол. Тогда, приравнивая ΔР и ρgh, получаем

h = 2σ cos θ/ρgr (5.28)

Если краевой угол θ тупой, величина h отрицательна, т.е. уровень жидкости в капилляре ниже, чем в жидкости.

5.4 Фазовые превращения.

Фазой называется макроскопическая, физически однородная часть вещества, отделённая от остальных частей системы границами раздела, так что она может быть извлечена из системы механическим путём. Фаза более мелкая категория, чем агрегатное состояние вещества, - в любом агрегатном состоянии, кроме газообразного, может быть многофазная система. Важнейшим вопросом в учении о фазах является выяснение условий, при которых система, состоящая из двух или нескольких фаз, находится в равновесии. Равенство давлений и температур ещё не означает, что система находится в равновесии, необходимо ещё равновесие по отношению к взаимным превращениям фаз. Как следует из (5.22) при постоянных температурах Т и давлениях Р термодинамический потенциал может только уменьшаться, т.к.

dФ ≤ 0. В состоянии равновесия значение Ф должно быть минимально. Рассмотрим систему, состоящую из двух фаз 1 и 2, которые могут превращаться друг в друга. Пусть m₁ и m₂ массы первой и второй фаз, а φ₁ и φ₂ – их удельные термодинамические потенциалы. Тогда для всей системы

Ф = m₁φ₁ + m₂φ₂ (5.29)

Если φ₁ > φ₂, то всякое превращение фазы 1 в фазу 2 сопровождается уменьшением Ф, это превращение будет происходить, пока вся фаза 1 не перейдёт в фазу 2. Наоборот, если φ₁ < φ₂, то фаза 2 в конце концов превратится в фазу 1. Только при условии φ₁ = φ₂ возможно равновесие. Таким образом, условием равновесия фаз является равенство их удельных термодинамических потенциалов. При изменении давления температура фазового равновесия также изменяется. Примерами фазовых превращений являются изменения агрегатного состояния вещества. Найдем, например, наклон кривой испарения. При смещении вдоль кривой испарения

dφ₁ = dφ₂, т.е.

v₁ dP – s₁ dT = v₂ dP – s₂ dT,

или

dP/dT = (s₁ – s₂)/(v₁ – v₂) (5/30)

где v и s - удельные объём и энтропия. При переходе из газообразного состояния 1 в жидкое состояние 2 выделяется количество тепла, - удельная теплота испарения q₁₂, поэтому

s₁ – s₂ = q₁₂/Т,

тогда

dP/dT = q₁₂/(T(v₁ – v₂)/ (5/31)

Это важное соотношение называется уравнением Клапейрона - Клаузиуса. Для кривой испарения воды dP/dT = 36 гПа/К.

Процесс интенсивного испарения, происходящий по всему объёму жидкости, называется кипением. Чтобы пузырёк, находящийся внутри жидкости на глубине h, расширялся, необходимо, чтобы давление насыщенного пара превышало сумму атмосферного, гидростатического и лапласова давления

Р_Н > Р_А + ρgh + 2σ/r (5.32)

При кипении жидкости, в неглубоком сосуде, если в ней имеются достаточно крупные пузырьки, вторым и третьим слагаемыми в правой части (5.32) можно пренебречь.

Дата добавления: 2015-03-31