
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 2
|
|
|
|
Решите уравнение 2|x2 + 2x – 5| = x – 1.
function changeDecision(proofobj, proofname) { if (proofobj.style.display=='none') { proofobj.style.display='inline'; proofname.innerHTML='Решение'; } else { proofobj.style.display='none'; proofname.innerHTML='Показать решение'; } } Решение
Этому уравнению соответствуют два уравнения 2(x2 + 2x – 5) = x – 1 и 2(x2 + 2x – 5) = 1 – x, среди корней которых нужно отобрать удовлетворяющие условию x ≥ 1. Имеем:
1.  Корни этого уравнения Корни этого уравнения 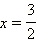 и x = –3, из которых подходит первый корень.
2. и x = –3, из которых подходит первый корень.
2.  Корни этого уравнения Корни этого уравнения  Опять подходит только первый корень, так как второй заведомо отрицателен.
Ответ. Опять подходит только первый корень, так как второй заведомо отрицателен.
Ответ.  
|

 В случае вложенных знаков модуля применим этот метод несколько раз. Здесь тоже можно рассмотреть весь набор получающихся при раскрытии модуля уравнений среди решений которых содержатся решения исходного уравнения, а потом отобрать из всех полученных решений подходящие хотя бы с помощью проверки.
В случае вложенных знаков модуля применим этот метод несколько раз. Здесь тоже можно рассмотреть весь набор получающихся при раскрытии модуля уравнений среди решений которых содержатся решения исходного уравнения, а потом отобрать из всех полученных решений подходящие хотя бы с помощью проверки.

|
   
|
6. Числовые функции. Определения. Способы задания. Операции над функциями. Композиция функций. Преобразования графиков функций.
функция — это закон, по которому каждому значению элемента x из некоторого множества X ставится в соответствие единственный элемент y из множества Y.
| П р и м е р. | Температура T кипения воды и атмосферное давление p связаны функциональной зависимостью, потому что каждому значению давления соответствует определённое значение температуры и наоборот. Так, если p = 1 бар, то T = 100° C; если p = 0.5 бар, то T = 81.6° C. |
Переменная, значения которой заданы, называется аргументом или независимой переменной; другая переменная, значения которой находятся по определённому правилу – называется функцией. Аргумент обычно обозначается через x, а функция – через y.
| П р и м е р. | Тело бросают вверх; h – его высота над землёй, t - время, прошедшее с момента бросания. h - однозначная функция t, но t - двузначная функция h, потому что тело попадает на одну и ту же высоту дважды: один раз при подъёме, другой раз при падении. Формула
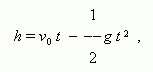 связывающая переменные h и t (начальная скорость v0 и ускорение свободного падения g здесь постоянны), показывает, что мы имеем только одно значение h при заданном t, и два значения t при заданном h (они определяются решением квадратного уравнения).
связывающая переменные h и t (начальная скорость v0 и ускорение свободного падения g здесь постоянны), показывает, что мы имеем только одно значение h при заданном t, и два значения t при заданном h (они определяются решением квадратного уравнения).
|
Многие из функций могут быть представлены (точно или приближённо) с помощью простых формул. Например, зависимость между площадью круга S и его радиусом r задаётся формулой S =  r 2; предыдущий пример показывает зависимость между высотой h брошенного тела и временем полёта t. Но эта формула практически приближённая, так как не учитывает ни сопротивления воздуха, ни уменьшения притяжения Земли с высотой. Очень часто невозможно представить функциональную зависимость с помощью формулы, или эта формула неудобна для вычислений. В этих случаях функцию представляют с помощью таблицы или графика.
r 2; предыдущий пример показывает зависимость между высотой h брошенного тела и временем полёта t. Но эта формула практически приближённая, так как не учитывает ни сопротивления воздуха, ни уменьшения притяжения Земли с высотой. Очень часто невозможно представить функциональную зависимость с помощью формулы, или эта формула неудобна для вычислений. В этих случаях функцию представляют с помощью таблицы или графика.
П р и м е р. Функциональную зависимость между давлением p и температурой T кипения воды невозможно представить одной формулой, но можно задать таблицей:
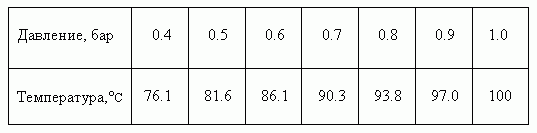
Очевидно, что любая таблица не может содержать все значения аргумента, но пригодная для практических целей таблица должна содержать столько значений, чтобы их было достаточно для работы или для получения дополнительных значений путём интерполяции уже содержащихся в ней.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 521; Нарушение авторских прав?; Мы поможем в написании вашей работы!