
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Обобщенное понятия угла и круговой дуги. Различные меры углов и дуг. Определение тригонометрических функций угла .Знаки тригонометрических функций. Формулы приведения
|
|
|
|
Градусная мера. Здесь единицей измерения является градус (обозначение °) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360°. Один градус состоит из 60 минут (их обозначение ‘); одна минута – соответственно из 60 секунд (обозначаются “).
Радианная мера. Как мы знаем из планиметрии (см. параграф «Длина дуги» в разделе «Геометрическое место точек. Круг и окружность»), длина дуги l, радиус r и соответствующий центральный угол  связаны соотношением:
связаны соотношением:
 = l / r.
= l / r.
Эта формула лежит в основе определения радианной меры измерения углов. Так, если l = r, то  = 1, и мы говорим, что угол
= 1, и мы говорим, что угол  равен 1 радиану, что обозначается:
равен 1 радиану, что обозначается:  = 1 рад. Таким образом, мы имеем следующее определение радианной меры измерения:
= 1 рад. Таким образом, мы имеем следующее определение радианной меры измерения:
Радиан есть центральный угол, у которого длина дуги и радиус равны (A m B = AO, рис.1). Итак, радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги.
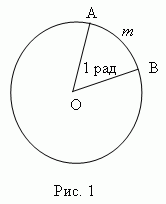
Следуя этой формуле, длину окружности C и её радиус r можно выразить следующим образом:
2  = C / r.
= C / r.
Так, полный оборот, равный 360° в градусном измерении, соответствует2  в радианном измерении. Откуда мы получаем значение одного радиана:
в радианном измерении. Откуда мы получаем значение одного радиана:
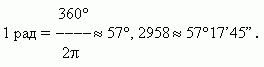
Обратно,
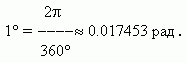
Полезно помнить следующую сравнительную таблицу значений наиболее часто встречающихся углов в градусах и радианах:

Тригонометрические функции острого угла есть отношения различных пар сторон прямоугольного треугольника (рис.2):
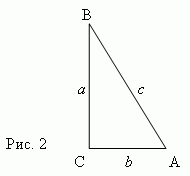
1) Синус - отношение противолежащего катета к гипотенузе: sin A = a / c.
2) Косинус - отношение прилежащего катета к гипотенузе: cos A = b / c.
3) Тангенс - отношение противолежащего катета к прилежащему: tan A = a / b.
4) Котангенс - отношение прилежащего катета к противолежащему: cot A = b / a.
5) Секанс - отношение гипотенузы к прилежащему катету: sec A = c / b.
6) Косеканс - отношение гипотенузы к противолежащему катету: cosec A = c / a.
Аналогично записываются формулы для другого острого угла B (Запишите их, пожалуйста!).
П р и м е р. Прямоугольный треугольник ABC (рис.2) имеет катеты:
a = 4, b = 3. Найти синус, косинус и тангенс угла A.
Р е ш е н и е. Во-первых, найдём гипотенузу, используя теорему Пифагора:
c 2 = a 2 + b 2,
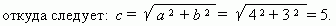
Согласно вышеприведенным формулам имеем:
sin A = a / c = 4 / 5; cos A = b / c = 3 / 5; tan A = a / b = 4 / 3.
Для некоторых углов можно записать точные значения их тригонометрических функций. Наиболее важные случаи приведены в таблице:

Углы 0° и 90°, строго говоря, не являются острыми в прямоугольном треугольнике, однако при расширении понятия тригонометрических функций (см. далее) эти углы также рассматриваются. Символ 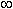 в таблице означает, что абсолютное значение функции неограниченно возрастает, если угол приближается к указанному значению.
в таблице означает, что абсолютное значение функции неограниченно возрастает, если угол приближается к указанному значению.
Чтобы построить всю тригонометрию, законы которой были бы справедливы для любых углов (не только для острых, но и для тупых, положительных и отрицательных углов), необходимо рассмотреть так называемый единичный круг, то есть круг, радиус которого равен 1 (рис.3).
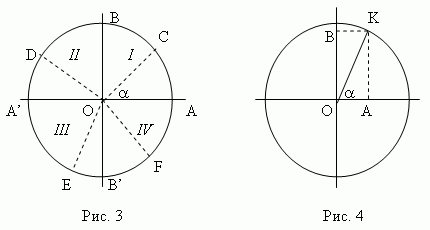
Проведём два диаметра: горизонтальный AA’ и вертикальный BB’. Будем отсчитывать углы от точки A (начальная точка). Отрицательные углы отсчитываются по часовой стрелке, положительные – против. Подвижный радиус OC образует угол  с неподвижным радиусом OA. Он может быть расположен в 1-ой четверти (COA), во 2-ой четверти (DOA), в 3-ей четверти (EOA) или в 4-ой четверти (FOA). Считая OA и OB положительными направлениями, а OA’ и OB’ – отрицательными, мы определим тригонометрические функции следующим образом.
с неподвижным радиусом OA. Он может быть расположен в 1-ой четверти (COA), во 2-ой четверти (DOA), в 3-ей четверти (EOA) или в 4-ой четверти (FOA). Считая OA и OB положительными направлениями, а OA’ и OB’ – отрицательными, мы определим тригонометрические функции следующим образом.
Линия синуса угла  (рис.4) - это вертикальный диаметр единичного круга, линия косинуса угла
(рис.4) - это вертикальный диаметр единичного круга, линия косинуса угла  - горизонтальный диаметр единичного круга. Синус угла
- горизонтальный диаметр единичного круга. Синус угла  (рис.4) – это отрезок OB на линии синуса, то есть проекция подвижного радиуса OK на линию синуса; косинус угла
(рис.4) – это отрезок OB на линии синуса, то есть проекция подвижного радиуса OK на линию синуса; косинус угла  - отрезок OA линии косинуса, то есть проекция подвижного радиуса OK на линию косинуса. Знаки синуса и косинуса в различных четвертях единичного круга показаны на рис.5 и рис.6.
- отрезок OA линии косинуса, то есть проекция подвижного радиуса OK на линию косинуса. Знаки синуса и косинуса в различных четвертях единичного круга показаны на рис.5 и рис.6.

Линия тангенса (рис.7) – это касательная к единичному кругу, проведенная через точку A горизонтального диаметра.
Линия котангенса (рис.8) – это касательная к единичному кругу, проведенная через точку В вертикального диаметра.
Тангенс – это отрезок линии тангенса между точкой касания A и точкой пересечения (D, E, и т.д., рис.7) линии тангенса и линии радиуса.
Котангенс – это отрезок линии котангенса между точкой касания В и точкой пересечения (Р, Q, и т.д., рис.8) линии котангенса и линии радиуса.
Знаки тангенса и котангенса в различных четвертях единичного круга показаны на рис.9.

Секанс и косеканс определяются как величины, обратные соответственно косинусу и синусу.
Точки максимума и минимума. Наибольшее и наименьшее значение функции на промежутке. Определения. Примеры.
Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если
f(x2) > f(x1) при x2 > x1.
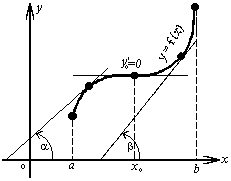 Рис.1 (а)
Рис.1 (а)
|
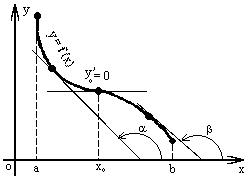 Рис.1 (б)
Рис.1 (б)
|
Из этого определения следует, что у возрастающей в интервале (a,b) функции f(x) в любой точке этого интервала приращения D x и D y имеют одинаковые знаки.
График возрастающей функции показан на рисунке 1(а).
Если из неравенства x2 > x1 вытекает нестрогое неравенство f (x2) ³ f (x1), то функция f (x) называется неубывающей в интервале (a, b). Пример такой функции показан на рисунке 2(а). На интервале [ x0, x1 ] она сохраняет постоянное значение C
Определение 2. Функция f (x) называется убывающей в интервале (a, b) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если
f(x2) < f(x1) при x2 > x1.
Из этого определения следует, что у убывающей в интервале (a, b) функции f (x) в любой точке этого интервала приращения D x и D y имеют разные знаки.
График убывающей функции показан на рисунке 1(б).
Если из неравенства x2 > x1 вытекает нестрогое неравенство f(x2) £ f(x1), то функция f (x) называется невозрастающей в интервале (a, b). Пример такой функции показан на рисунке 2(б). На интервале [ x0, x1 ] она сохраняет постоянное значение C.

Рассмотрим график непрерывной функции y=f(x), изображенной на рисунке. Значение функции в точке x 1 будет больше значений функции во всех соседних точках как слева, так и справа от x 1. В этом случае говорят, что функция имеет в точке x 1 максимум. В точке x 3 функция, очевидно, также имеет максимум. Если рассмотреть точку x 2, то в ней значение функции меньше всех соседних значений. В этом случае говорят, что функция имеет в точке x 2 минимум. Аналогично для точки x 4.
Функция y=f(x) в точке x 0 имеет максимум, если значение функции в этой точке больше, чем ее значения во всех точках некоторого интервала, содержащего точку x 0, т.е. если существует такая окрестность точки x 0, что для всех x ≠ x 0, принадлежащих этой окрестности, имеет место неравенство f(x) < f(x 0 ).
Функция y=f(x) имеет минимум в точке x 0, если существует такая окрестность точки x 0, что для всех x ≠ x 0, принадлежащих этой окрестности, имеет место неравенство f(x) > f(x0.
Точки, в которых функция достигает максимума и минимума, называются точками экстремума, а значения функции в этих точках экстремумами функции.
Обратим внимание на то, что функция, определенная на отрезке, может достигать максимума и минимума только в точках, заключенных внутри рассматриваемого отрезка.
Отмети, что если функция имеет в точке максимум, то это не означает, что в этой точке функция имеет наибольшее значение во всей области определения. На рисунке, рассмотренном выше, функция в точке x 1 имеет максимум, хотя есть точки, в которых значения функции больше, чем в точке x 1. В частности, f (x 1) < f (x 4) т.е. минимум функции больше максимума. Из определения максимума следует только, что это самое большое значение функции в точках, достаточно близких к точке максимума.
Наибольшее и наименьшее значения функции- понятия математического анализа. Значение, принимаемое функцией в некоторой точке множества, на котором эта функция задана, называется наибольшим (наименьшим) на этом множестве, если ни в какой другой точке множества функция не имеет большего (меньшего) значения. Н. и н. з. ф. по сравнению с её значениями во всех достаточно близких точках называются экстремумами (соответственно максимумами и минимумами) функции. Непрерывная функция, заданная на отрезке, обязательно достигает на нём наибольшего и наименьшего значений; если же непрерывную функцию рассматривать на интервале (т. е. отрезке с исключенными концами), то среди её значений на этом интервале может не оказаться наибольшего или наименьшего. Например, функция у = x, заданная на отрезке [0; 1], достигает наибольшего и наименьшего значений соответственно при x = 1 и x = 0 (т. е. на концах отрезка); если же рассматривать эту функцию на интервале (0; 1), то среди её значений на этом интервале нет ни наибольшего, ни наименьшего, так как для каждого x0 всегда найдётся точка этого интервала, лежащая правее (левее) x0, и такая, что значение функции в этой точке будет больше (соответственно меньше), чем в точке x0. Аналогичные утверждения справедливы для функций многих переменных.
Множество точек на плоскости. Подмножества. Пересечение и объединение множеств.
Практическая часть
Дополнительные вопросы при ответе на билет.
ü Сделайте заключение о количестве корней трехчлена 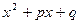 , если
, если  и
и 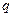 удовлетворяют неравенству
удовлетворяют неравенству 
ü Определить  , если
, если  ,
, 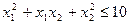 , где
, где 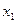 и
и 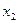 - корни функции.
- корни функции.
ü Изобразите множество точек на координатной плоскости 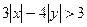
ü Изобразите множество точек на координатной плоскости 
ü Четные и нечетные функции. (№ 100)
ü 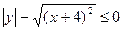 , Изобразить множество точек на координатной плоскости
, Изобразить множество точек на координатной плоскости
ü Постройте график функции 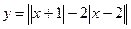
ü Постройте произвольный график функции и выполните преобразование 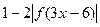
ü Постройте множество плоскости для которых 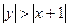
ü В отделе института работают несколько человек. Каждый из них знает хотя бы один иностранный язык. 6- человек знает английский, 6- немецкий, семь французский, 4- знают английский и немецкий, 3- немецкий и французский. 2- французский и английский. 1- человек знает все три языка. Сколько человек работает в отделе? Сколько из них знает только английский язык? Только французский? Сколько человек знает ровно один язык?
ü Нормандское окно имеет форму прямоугольника, завершенное полукругом. Периметр окна равен а. каковы должны быть размеры окна, чтобы окно пропускало наибольшее количество света?
ü На плоскости рОq изобразить множество точек для которых
х²+ (р-1)+ q +2 а) Имеет различные корни б) не имеет корней в) имеет один корень.
ü 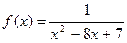 , исследовать и построить график функции.
, исследовать и построить график функции.
ü 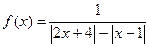 , исследовать и построить график функции.
, исследовать и построить график функции.
ü  , исследовать и построить график функции.
, исследовать и построить график функции.
ü Определите а так, чтобы сумма квадратов корней уравнения была наименьшей. 
ü 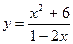 , исследовать и построить график функции.
, исследовать и построить график функции.
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 4305; Нарушение авторских прав?; Мы поможем в написании вашей работы!