Обозначение функций

Пусть y - некоторая функция переменной x; причём, неважно, каким образом эта функция задана: формулой, таблицей или как-то иначе. Важен только сам факт существования этой функциональной зависимости, что записывается следующим образом: y = f (x). Буква f (начальная буква латинского слова “functio”- функция) не обозначает какой-либо величины, так же как буквы log, sin, tan в записях функций y = log x, y = sin x, y = tan x. Они говорят лишь об определённых функциональных зависимостях y от x. Запись y = f (x) представляет любую функциональную зависимость. Если две функциональные зависимости: y от x и z от t отличаются одна от другой, то они записываются с помощью различных букв: y = f (x) и z = F (t). Если же некоторые зависимости одни и те же, то они записываются одной и той же буквой f: y = f (x) и z = f (t). Если выражение для функциональной зависимости y = f (x) известно, то она может быть записана с использованием обоих обозначений функции. Например, y = sin x или f (x) = sin x. Обе формы полностью равносильны. Иногда используется и другая форма записи: y (x). Это означает то же самое, что и y = f (x).

Графическое представление функций.

Чтобы представить функцию y = f (x) в виде графика, нужно:

1) Записать ряд значений функции и её аргумента в таблицу:

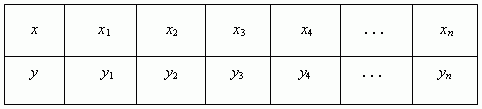
2) Перенести координаты точек функции из таблицы в систему координат,

отметив в соответствии с выбранным масштабом значения абсцисс на

оси Х и значения ординат на оси Y (рис.2). В результате в нашей системе

координат будет построен ряд точек A, B, C,..., F.

3) Соединяя точки A, B, C,..., F плавной кривой, получаем график заданной

функциональной зависимости.

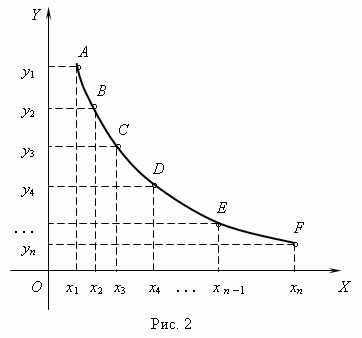
Такое графическое представление функции даёт наглядное представление о характере её поведения, но достигаемая при этом точность недостаточна. Возможно, что промежуточные точки, не построенные на графике, лежат далеко от проведенной плавной кривой. Хорошие результаты в значительной степени зависят также от удачного выбора масштабов. Поэтому следует определить график функции как геометрическое место точек, координаты которых M (x, y) связаны заданной функциональной зависимостью.

Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R. Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т.e. она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента x, при которых функция y = f (x)определена, называется областью определения функции. Множество Y всех действительных значений y, которые принимает функция, называется областью значений функции. Теперь можно дать более точное определение функции: правило (закон) соответствия между множествами X и Y, по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y, называется функцией.

Из этого определения следует, что функция считается заданной, если:

- задана область определения функции X;

- задана область значений функции Y;

- известно правило (закон) соответствия, причём такое, что для каждого

значения аргумента может быть найдено только одно значение функции.

Это требование однозначности функции является обязательным.

Монотонная функция. Если для любых двух значений аргумента x ₁ и x ₂ на интервале I из условия x ₂> x ₁ следует f (x ₂) > f (x ₁ ), то функция f (x)называется возрастающей; если для любых x ₁ и x ₂ на интервале I из условия x ₂> x ₁ следует f (x ₂) < f (x ₁), то функция f (x) называется убывающей. Функция, которая только возрастает или только убывает, называется монотонной.

Ограниченная и неограниченная функции. Функция называется ограниченной, если существует такое положительное число M, что | f (x) | 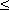M для всех значений x. Если такого числа не существует, то функция - неограниченная.

П р и м е р ы.

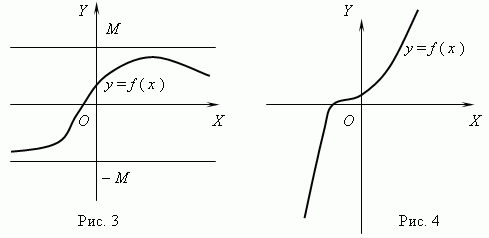
Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 - как раз наоборот, монотонная, но неограниченная. (Объясните это, пожалуйста!).

Непрерывная и разрывная функции. Функция y = f (x) называется непрерывной в точке x = a, если:

1) функция определена при x = a, т.e. f (a) существует;

2) существует конечный предел lim f (x);

x → a

3) f (a) = lim f (x).

x → a

Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a. Если функция непрерывна во всех точках своей области определения, то она называется непрерывной функцией.

Чётная и нечётная функции. Если для любого x из области определения функции имеет место: f ( x) = f (x), то функция называется чётной; если же имеет место: f ( x) =  f (x), то функция называется нечётной. График чётной функции симетричен относительно оси Y (рис.5), a график нечётной функции симметричен относительно начала координат (рис.6).

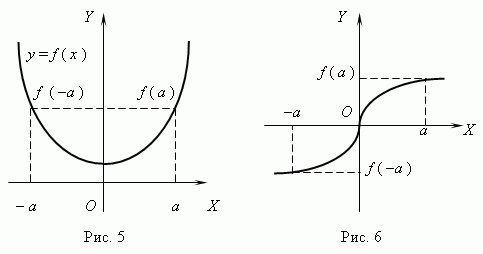
Периодическая функция. Функция f (x) - периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f (x + T) = f (x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими.

П р и м е р 1. Доказать, что sin x имеет период 2 

Р е ш е н и е. Мы знаем, что sin (x+ 2 n) = sin x, где n = 0,  1,  2, …

Следовательно, добавление 2 n к аргументу синуса не меняет его значениe. Существует ли другое число с таким

же свойством? Предположим, что P – такое число, т.e. равенство:

sin (x+ P) = sin x,

справедливо для любого значения x. Но тогда оно имеет место и при x = / 2, т.e. sin ( / 2 + P) = sin / 2 = 1.

Но по формуле приведения sin ( / 2 + P) = cos P. Тогда из двух последних равенств следует, что cos P = 1, но мы знаем, что это верно лишь при P = 2 n. Так как наименьшим отличным от нуля числом из 2 n является 2 , то это число и есть период sin x. Аналогично доказывается, что 2 является периодом и для cos x. Докажите, что функции tan x и cot x имеют период .

П р и м е р 2. Какое число является периодом функции sin 2 x?

Р е ш е н и е. Рассмотрим sin 2 x = sin (2 x + 2 n) = sin [ 2 (x + n 

Мы видим, что добавление n к аргументу x, не меняет

значение функции. Наименьшее отличное от нуля число

из n есть таким образом, это период sin 2 x.

Нули функции. Значение аргумента, при котором функция равна 0, называется нулём (корнем) функции. Функция может иметь несколько нулей.Например, функция y = x (x + 1) (x 3) имеет три нуля: x = 0, x = 1, x = 3. Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х.

На рис.7 представлен график функции с нулями: x = a, x = b и x = c.

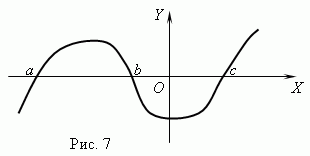
Асимптота. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой.

Дата добавления: 2015-04-23