Билет 18

1.Квантовомеханическое объяснение строения атома. Характеристика энергетического состояния ē квантовыми числами. Атомные орбитали. Принцип наименьшей энергии. Принцип Паули. Правило Хунда.

Согласно волновой теории, ē является и частицей и волной, т.е. проявляет корпускулярно-волновой дуализм, который для электрона предложил Л. де Бройль: *корпускулярные сво-ва ē выражаются в его способности проявлять свое действие только как целого;*волновые сво-ва проявляются в его движении, а также в явлениях дифракции и интерференции.

ē как бы размазан вокруг ядра по сфере, удаленной от ядра на некоторое расстояние, таким образом, вместо стационарных орбит по Бору, ядро атома окружено пульсирующим ē-ым облаком- распространенным в пространстве заряде ē. Область пространства вокруг ядра, занимаемая ē-ми получила назв. - атомная орбиталь, выражающая форму электронного облака.

Атомная орбиталь – часть ē-го облака, где вероятность нахождения ē-на составляет 90%.Характеризуется конкретными значениями квантовых чисел: n,m,l,s. Форма: S-облако – 2 вида, Р–облако – 6 видов;d-облако – 10 видов;f-облако – 14 видов.

Понятие о квантовых числах – n, l, m,m – квантовые числа. В простейших приложениях квантовой механики иногда удобнее вместо самой волновой функции пользоваться квантовыми числами, представляющими её. Такой подход часто применяют для объяснения свойств многоэлектронных металлов. В настоящее время считается, что состояние каждого электрона в aтоме определяется с помощью четырех квантовых чисел

Первое из них называется главным квантовым числом. Главное квантовое число характеризует энергию электрона в атоме. Оно обозначается буквой "n" и принимает значения простых целых чисел (n =1,2,3…∞). Главное квантовое число характеризует оболочку (энергетический уровень), в которой находится электрон, определяет энергию электрона, степень удаленности от ядра, размеры электронной орбитали. Электроны, имеющие одинаковое значение n находятся на одном электронном и энергетическом уровне.

Второе квантовое число называется орбитальным. Орбитальное квантовое число (l) характеризует подоболочку (энергетический подуровень), на которой находится электрон.

Оно обозначается буквой l и принимает значения от 0 до n -1. Орбитальное квантовое число определяет орбитальный момент импульса электрона M, а также пространственную форму электронной орбитали(угловую зависимость волновой функции). Электроны имеющие одинаковое значение l находятся на одном электронном подуровне.

Третье квантовое число называется магнитным. Магнитное квантовое число (m) характеризует расположение в пространстве орбитали, на которой находится электрон.Оно обозначается M или М_e и принимает значения от - l до + l включая 0. Магнитное квантовое число определяет значения проекции орбитального момента на одну из осей, а такжe пространственную ориентацию элементарных орбиталей и их максимальное число на электронном подуровне

Четвертое квантовое число называется спиновым квантовым числом. Спиновое квантовое число (s) характеризует собственный магнитный момент электрона. Оно обозначается М_s или S и может принимать два значения m_s = + ¹/₂ или - ¹/₂. Наличие спинового квантового числа объясняется тем, что электрон обладает собственным моментом импульса ("спином"), не связанным с перемещением в пространстве вокруг ядра.

Основное состояние атома – состояние атома когда его электроны находятся на таких энергетических уровнях, что их суммарная энергия в атоме является минимальной из возможных значений энергии (принцип наименьшей энергии). Это значит, что при заполнении электронами орбиталей в многоэлектронном атоме в первую очередь заполняются все максимально возможные свободные орбитали с наименьшей энергией. Состояния с более высокими значениями энергией называют возбужденными, а сам процесс или результат повышения энергии атома(или электрона) – возбуждением.

Швейцарский ученый Вольфганг Паули сформулировал принцип заполнения электронных орбиталей. В атоме не может быть двух электронов с одинаковым значением всех четырех квантовых чисел. Это означает, что на каждой электронной орбитали может максимум находиться два электрона, имеющих различные значения спинового квантового числа (антипараллельные спины). Принцип Паули позволяет определить не только максимальную емкость электронной орбитали, но и уровнeй целом

Заполнение электронами орбиталей внутри подуровня происходит в соответствии с правилом, сформулированным немецким физиком Фридериком Хундом, чтобы алгебраическое значение суммарного спина было максимальным, т.е. внутри подуровней электроны заполняют все максимально возможные свободные орбитали

Правило Клечковского: Заполнение электронами орбиталей в атоме происходит в порядке возрастания суммы главного и орбитального квантовых чисел . При одинаковой сумме раньше заполняется орбиталь с меньшим значением .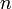

Дата добавления: 2015-04-23