Уравнение прямой проходящей через две точки. Параметрические уравнения прямой

Уравнение прямой, проходящей через две различные точки (х ₁, у ₁) и (х ₂, у ₂ ):

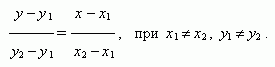
Параметрическое уравнение прямой, проходящей через точку (х ₀ , у ₀) и параллельной направляющему вектору прямой (a, b):

20. Прямая как линия пересечения двух плоскостей.

Пусть заданы две плоскостиАх+ Ву+ Сz+ D = 0 и Eх+ Fу+ Gz+ H = 0, причём их нормальные векторы неколлинеарны, тогда система уравнений

описывает прямую – линию пересечения этих плоскостей.

при условии, что не имеет место равенство

A1	=	B1	=	C1	.
A2	B2	C2

21 Взаимное расположение двух прямых в пространстве.

Взаимное расположение двух прямых в пространстве

Взаимное расположение двух прямых и пространстве характеризуется следующими тремя возможностями. 1. Прямые лежат в одной плоскости и не имеют общих точек — параллельные прямые. 2. Прямые лежат и одной плоскости и имеют одну общую точку — прямые пересекаются. 3. В пространстве две прямые могут быть расположены еще так, что не лежат ни в одной плоскости. Такие прямые называются скрещивающимися (не пересекаются и не параллельны). Теорема. Если одна из двух прямых лежит в некоторой плоскости, а другая пересекает эту плоскость и точке, которая не лежит на первой прямой, то эти прямые скрещиваются. На рис. 26 прямая a лежит в плоскости , а прямая с пересекает в точке N. Прямые a и с — скрещивающиеся. Теорема. Через каждую из двух скрещивающихся прямых проходит только одна плоскость, параллельная другой прямой. 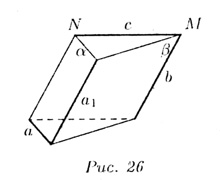На рис. 26 прямые a и b скрещиваются. Черен прямую а проведена плоскость || b (в плоскости указана прямая a₁ || b). Примеры скрещивающихся прямых: трамвайный рельс и троллейбусный провод по пересекающейся улице, нeпересекающиеся и непараллельные ребра пирамид или призм и пр. Все три случая можно видеть еще на примере прямых, по которым встречаются стены и потолок или стены и пол комнаты.

22. Вычисление углов в пространстве

Понятие о скалярном произведении позволяет достаточно просто определять углы между прямыми в пространстве. Действительно, пусть в пространстве заданы две прямые с направляющими векторами и 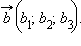Пусть угол между этими прямыми равен φ. Тогда угол между векторами может быть равен φ или 180° – φ в зависимости от того, как направлены эти вектора. Однако в любом случае модуль скалярного произведения этих векторов равен

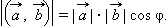
Отсюда следует, что 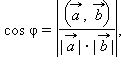так как Итак, угол между двумя прямыми может быть найден через координаты направляющих векторов так

Покажем теперь, как можно вычислять угол между прямой и плоскостью. Поскольку угол между прямой и плоскостью есть угол между этой прямой и ее проекцией на эту плоскость, сведем данную задачу к предыдущей. Заметим, что угол между направляющим вектором рассматриваемой прямой и нормальным вектором равен

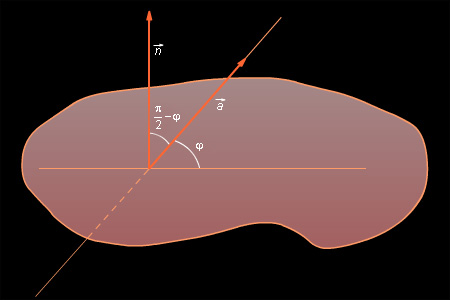
Рисунок 9.9.1

Этот угол уже легко вычисляется: Значит угол между прямой и плоскостью равен

Найдем, наконец, угол между двумя плоскостями, если известны их нормальные векторы. Несложно сообразить, что угол между плоскостями равен углу между их нормалями.

Значит, угол между плоскостями может быть найден по формуле:

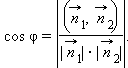
Дата добавления: 2015-04-23