
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Колебания и волны
|
|
|
|
Классификация магнетиков
| μ < 1, не зависит от температуры | - | диамагнетики (вода, медь, графит, кварц) 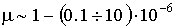 , ,
|
| μ > 1, зависит от температуры | - | парамагнетики (алюминий, платина, натрий) 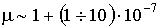 при T ≈ 300 K, при T ≈ 300 K,
|
| μ >> 1, зависит от температуры и нелинейно от поля B0 | - | ферромагнетики (железо, никель, кобальт) 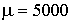 для Fe, при T ≈ 300 K, при для Fe, при T ≈ 300 K, при 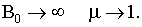
|
12. Диамагнетики - по закону Фарадея-Ленца (11.10.1) при внесении в магнитное поле 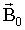 любого вещества в атомах вещества возникают внутренние токи, создающие магнитное поле
любого вещества в атомах вещества возникают внутренние токи, создающие магнитное поле  , направленное навстречу внешнему полю
, направленное навстречу внешнему полю  . В результате поле в веществе ослабляется. Если в веществе кроме этого отсутствуют другие магнитные эффекты, то оно будет диамагнетиком. Диамагнетизм проявляется у вещества, атомы которых не имеют собственного магнитного момента (11.8.1.1.),
. В результате поле в веществе ослабляется. Если в веществе кроме этого отсутствуют другие магнитные эффекты, то оно будет диамагнетиком. Диамагнетизм проявляется у вещества, атомы которых не имеют собственного магнитного момента (11.8.1.1.),
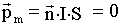
12. Парамагнетизм проявляется у веществ, атомы которых имеют собственный магнитный момент. Магнитные моменты 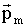 атомов выстраиваются по полю
атомов выстраиваются по полю 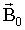 .
.
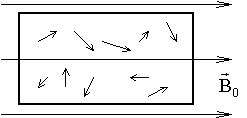
| Тепловые колебания атомов нарушают ориентацию магнитных моментов. |
12. Ферромагнетизм - объясняется самопроизвольным упорядочением спиновых магнитных моментов электронов в пределах областей спонтанного намагничивания (доменов).
В пределах одного домена магнитные моменты электронов ориентированы в одном направлении. Магнитные моменты разных доменов в отсутствии внешнего поля ориентированы по разному, так, чтобы энергия созданного ими поля была минимальная:
| а) | 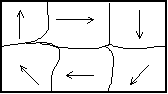
| 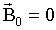
|
При включении внешнего поля расширяются за счет соседей те домены, которые ориентированы по полю:
| б) | 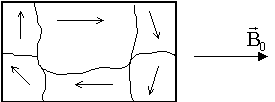
|
| в) | 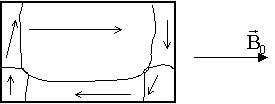
|
Затем переориентируются оставшиеся домены, и ферромагнетик намагничивается до насыщения:
| г) | 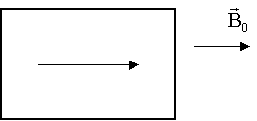
|
В результате этого зависимость поля в ферромагнетике  от переменного внешнего поля
от переменного внешнего поля 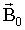 имеет вид петли гистерезиса, которую изображают в осях B-H.
имеет вид петли гистерезиса, которую изображают в осях B-H.
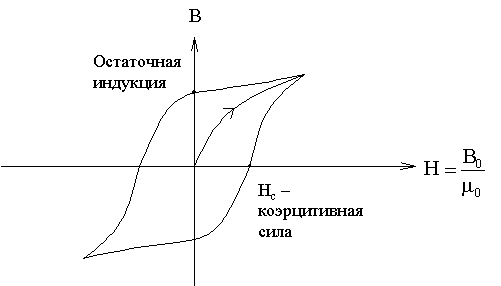
Вектор  называется вектором напряженности магнитного поля. Он носит вспомогательный характер, силовой характеристикой магнитного поля является вектор магнитной индукции
называется вектором напряженности магнитного поля. Он носит вспомогательный характер, силовой характеристикой магнитного поля является вектор магнитной индукции  (11.3). Связь между векторами
(11.3). Связь между векторами  и
и  записывается следующим образом:
записывается следующим образом:
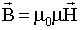 .
.
1. Гармонические колебания - периодический процесс, в котором рассматриваемый параметр изменяется по гармоническому закону. Если на колебательную систему не действуют внешние переменные силы, то такие колебания называются свободными. Рассмотрим массу, которая колеблется на пружине как показано на рисунке. Если амплитуда колебаний мала, то координата x массы по вертикальной оси изменяется по гармоническому закону:
x = A sin(w t + j)
где A - амплитуда колебаний, t - время, j - фаза колебаний,w- угловая частота колебаний,w= 2 p f = 2 p / T, f - частота колебаний, T - период колебаний.
Далее мы найдём период колебаний T пружинного маятника, состоящего из грузика массой m и пружины жёсткостью k. Если грузик смещён из нулевого положения (в котором пружина не деформирована) на расстояние x, то на грузик со стороны пружины будет действовать сила- kx. Помимо этого на грузик действует сила тяжести mg. Согласно второму закону Ньютона, сумма всех сил, приложенных к грузику, равна ma, где a - ускорение. Таким образом, мы можем записать дифференциальное уравнение для пружинного маятника:
m d2 x /d t 2 = - kx + mg
где g - ускорение свободного падения в гравитационном поле,d2 x /d t 2 - вторая производная координаты x по времени t. Это уравнение имеет следующее решение:
x = A sin[(k / m)1/2 t + j] + mg / k
Мы можем видеть из этой формулы, что период колебаний равен
T = 2p(m / k)1/2
и, соответственно, угловая частота w равна
w = (k / m)1/2
Амплитуда колебаний A и фаза колебаний j зависят от начальных условий (в момент времени t =0): начального смещение грузика x 0 и начальной скорости v 0. В состоянии равновесия пружина растянута на величину mg / k.
Предположим, что колеблющийся грузик связан с пером, который рисует линию на бумажной ленте. Если лента движется равномерно в горизонтальном направлении, то перо будет рисовать на ней синусоиду. Зная скорость движения ленты и период синусоиды, мы можем вычислить период колебаний грузика на пружине.
В общем случае на осциллятор действует сила трения, пропорциональная скорости движения грузика: F=av. В случае пружинного маятника эта сила возникает из-за сопротивления воздуха и неупругих свойств самого материала, из которых изготовлена пружина. В результате, амплитуда колебаний будет со временем уменьшаться. Уравнение свободного гармонического осциллятора с затуханием может быть записано следующим образом:
m (d2 x /d t 2) + a (d x /d t) + kx = mg
где a - коэффициент трения. Это уравнение может быть переписано в виде
d2 x /d t 2+ 2g(d x /d t) + W2 x = g
где 2g = a / m; W2= k / m
В случае, когда W2 > g2 уравнение колебаний свободного гармонического осциллятора с затуханием имеет следующее решение:
x = A e-g t cos(w t + j)
При этом период колебаний зависит от коэффициента затухания g:
T = 2p/w= 2p/(W2 -g2)1/2
|
|
|
|
|
Дата добавления: 2015-04-23; Просмотров: 496; Нарушение авторских прав?; Мы поможем в написании вашей работы!