КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Действия с линейными преобразованиями. Связь между матрицами линейного преобразования в различных базисах
|
|
|
|
№122. Дано линейное преобразование х/ = х + у + z, y/ = x + y, z/ = x и в системе координат х/ у/ z/ задана точка (3, –2, –1). Определить координаты этой точки в системе хуz.
Ответ: (-1; -1; 5).
№123. Даны два линейных преобразования: 
и 
Найти точки, для которых каждое из этих преобразований дает один и тот же результат.
Ответ: (t; t; 2t), 
.
№124. Дано линейное преобразование: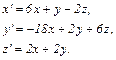 
Координаты каких точек удваиваются в результате этого преобразования?
Ответ: (t; 2t; 3t), 
.
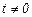№125. Найти множество точек, координаты которых меняются местами при применении линейного преобразования 
Ответ: Прямая линия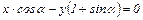 
.
№126. Даны линейные преобразования А и В соответственно: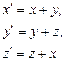 
и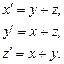 
Найти преобразования 3А – 2 В и АВ.
Ответ: 
; 
.
№127. Является ли линейным преобразованием замена каждого геометрического вектора его зеркальным отражением относительно координатной плоскости ху? Ответ обосновать.
Ответ: Да.
№128. Дано линейное преобразование f векторов в трехмерном пространстве – поворот вокруг оси z на угол α. Выразить координаты вектора – образа 
через координаты вектора – прообраза 
.
Ответ: 
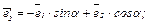
Указание: смотри примеры в § 2.
№129. Найти матрицу обратного для А 
= 
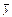преобразования, если А =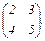 
Ответ: 
№130. Дано линейное преобразование: 
Найти матрицу обратного линейного преобразования.
Ответ: 
№131. В линейном пространстве с базисом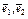 
дано линейное преобразование А. Найти матрицу обратного преобразования, если 
Ответ: 
№132. Линейное преобразование переводит базис 
в векторы 
соответственно. Составить матрицу линейного преобразования. Найти образ вектора 
.
Ответ: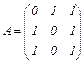 
; 
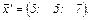
№133. Матрица линейного преобразования в базисе 
имеет вид 
. Найти образ вектора 
.
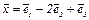Ответ: 
№134. В базисе 
преобразование f имеет матрицу А. Найти матрицу В преобразования f в базисе 
, 
, 
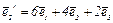, если 
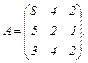
Ответ: 
№135. Дано линейное пространство многочленов степени не выше n: 
В качестве базиса выбраны функции 
так, что координатами вектора 
являются коэффициенты а0, а1, …, аn. Рассматривается дифференцирование многочленов – линейное преобразование в данном пространстве. Составить матрицу этого линейного преобразования.
Ответ: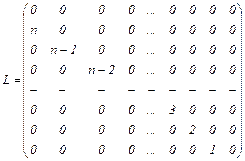 
.
№136. В двухмерном пространстве геометрических векторов на плоскости ху задано линейное преобразование, переводящее вектор (х1; х2) в симметричный относительно оси х вектор (х1; -х2). Найти матрицу этого преобразования в базисе 
и в базисе, состоящем из векторов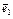 
= (1; 2) и 
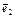= (-2; 1).
Ответ: 
.
№137. В трехмерном пространстве геометрических векторов задано линейное преобразование, переводящее вектор 
) в векторное произведение 
, где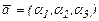 
. Найти матрицу этого преобразования в базисе 
и в базисе, состоящем из векторов 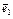= (0; 1; -1) 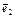= (1; 0; 1) и 
= (-1; 1; 0).
Ответ: 
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1456; Нарушение авторских прав?; Мы поможем в написании вашей работы!