Преобразование матрицы линейного преобразования при переходе к новому базису

ЛИНЕЙНЫЕ ПРЕОБРАЗОВАНИЯ. Матрица линейного преобразования конечномерного векторного пространства. Собственные значения и собственные векторы линейного преобразования, теорема о связи собственных значений линейного преобразования с корнями его характеристического многочлена.

Будем говорить, что на множестве векторов R задано преобразование А, если каждому вектору х 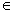R по некоторому правилу поставлен в соответствие вектор А х 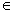R.

Определение 1.1. Преобразование А называется линейным, если для любых векторов х и у и для любого действительного числа λ выполняются равенства:

А(х + у)= А х + А у, А(λ х) = λ А х. (1.1)

Определение 1.2. Линейное преобразование называется тождественным, если оно преобразует любой вектор х в самого себя.

Тождественное преобразование обозначается Е: Е х = х.

Рассмотрим трехмерное пространство с базисом е₁, е₂, е₃, в котором задано линейное преобразование А. Применив его к базисным векторам, мы получим векторы А е₁, А е₂, А е₃, принадлежащие этому трехмерному пространству. Следовательно, каждый из них можно единственным образом разложить по векторам базиса:

А е₁ = а₁₁ е₁ + а₂₁ е₂ +а₃₁ е₃,

А е₂ = а₁₂ е₁ + а₂₂ е₂ + а₃₂ е₃, (1.2)

А е₃ = а₁₃ е₁ + а₂₃ е₂ + а₃₃ е₃.

Матрица 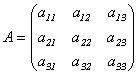называется матрицей линейного преобразования А в базисе е₁, е₂, е_{3 .} Столбцы этой матрицы составлены из коэффициентов в формулах (1.2) преобразования базиса.

Замечание. Очевидно, что матрицей тождественного преобразования является единичная матрица Е.

Для произвольного вектора х =х₁ е₁ + х₂ е₂ + х₃ е₃ результатом применения к нему линейного преобразования А будет вектор А х, который можно разложить по векторам того же базиса: А х =х`<sub>1</sub> е<sub>1</sub> + х`₂ е₂ + х`<sub>3</sub> е<sub>3</sub>, где координаты x`_i можно найти по формулам:

х`₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃,

x`₂ = a₂₁x₁ + a₂₂x₂ + a₂₃x₃, (1.3)

x`₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃.

Коэффициенты в формулах этого линейного преобразования являются элементами строк матрицы А.

Рассмотрим линейное преобразование А и два базиса в трехмерном пространстве: е₁, е₂, е₃ и е ₁, е ₂, е _{3 .} Пусть матрица С задает формулы перехода от базиса { e _k } к базису { e _k }. Если в первом из этих базисов выбранное линейное преобразование задается матрицей А, а во втором – матрицей А, то можно найти связь между этими матрицами, а именно:

А = С^-1 А С (1.4)

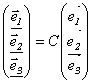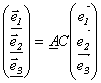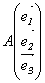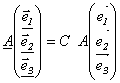Действительно, , тогда А . С другой стороны, результаты применения одного и того же линейного преобразования А в базисе { e _k }, т.е. , и в базисе { e _k }: соответственно - связаны матрицей С: , откуда следует, что СА= А С. Умножая обе части этого равенства слева на С ^-1, получим С ^{- 1} СА = = С ^-1 А С, что доказывает справедливость формулы (1.4).

Дата добавления: 2015-04-24