Евклидовы и унитарные пространства. Теорема об ортогонализации. Ортонормированный базис

Если длина вектора равна единице, он называется нормированным вектором: (x, x) = 1, |x| = 1.

Если все векторы системы векторов нормированы, то система векторов называется нормированной системой.

Если векторы системы векторов e ₁, e ₂, ..., e _n попарно ортогональны и нормированы, то система векторов называется ортонормированной системой: (e _i, e _j) = 0, если i ≠ j, (e _i, e _i ) = 1.

Если e ₁, e ₂, ..., e _n — ортонормированная система и x = x ₁ e₁ + x ₂ e₂ +... + x _n e _n — разложение вектора x по этой системе, то x _i =(x, e _i ).

Ортонормированная система, состоящая из n векторов n -мерного евклидова пространства, образует базис этого пространства. Такой базис называется ортонормированным базисом.

Если e ₁, e ₂, ..., e _n — ортонормированный базис n -мерного евклидова пространства и

x = x ₁ e₁ + x ₂ e₂ +... + x _n e _n — разложение вектора x по этому базису, то координаты x _i вектора x в ортонормированном базисе вычисляются по формулам x _i =(x, e _i ), i = 1, 2,..., n.

Теорема 1.1 (об ортогонализации) В евклидовом пространстве любой базис может быть преобразован к ортонормированному базису.

Доказательство. Пусть дан произвольный базис в мерном евклидовом пространстве:

Построим следующие системы, 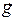и 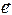векторов:

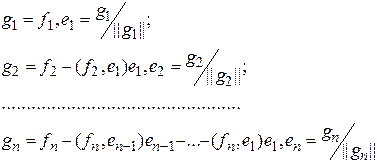
Докажем, что система 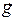ортогональна (тогда ясно, что система 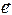ортонормированная). Доказательство проведем индукцией по . Базис индукции очевиден, так как система, состоящая из одного ненулевого вектора, ортогональна по определению. Пусть для некоторого 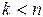подсистема ортогональна. Вычислим скалярное произведение для произвольного .

Имеем:

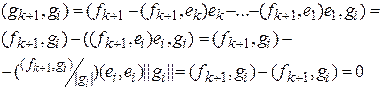
(мы учли, что для любого скалярное произведение ).

Итак, система 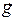ортогональна, и теорема доказана.

Базис конечномерного евклидова пространства называется ортонормированным базисом, если образующие его векторы попарно ортогональны и имеют единичную длину. Поскольку доказано, что в любом конечномерном евклидовом пространстве существует ортонормированный базис, будем рассматривать в -мерном евклидовом пространстве 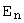только ортонормированные базисы.

Простейший пример евклидова пространства дает нам пространство -- пространство столбцов, в котором скалярное произведение введено формулой .

Тогда для любых , из справедливы формулы:

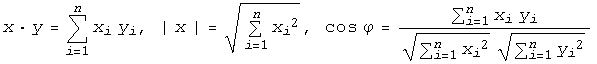
Все евклидовы пространства размерности устроены так же, как пространство .

Величины , 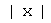и характеризуют взаимное расположение векторов и не зависят от выбранного ортонормированного базиса.
Если и 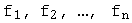-- два ортонормированных базиса в -мерном евклидовом пространстве, то матрица перехода от одного из этих базисов к другому -- ортогональная матрица.

Дата добавления: 2015-04-24