Понятие линейного пространства

ЛИНЕЙНЫЕ ВЕКТОРНЫЕ ПРОСТРАНСТВА И СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ (С.Л.У.). Линейная зависимость и независимость систем векторов. Подпространства. Линейная оболочка системы векторов. Базис и размерность. Теорема о размерности суммы двух подпространств. Теорема о размерности пространства решений однородной С.Л.У.

Множество L называется линейным (векторным) пространством, если выполнены следующие условия:

1) В L введена операция сложения элементов, т.е. 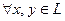определено отображение (обозначение: 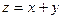), обладающее следующими свойствами:

- ;

- ;

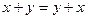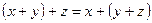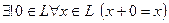- (элемент 0 называется нулевым);

- (элемент – x называется противоположным элементу x);

2) В L введена операция умножения элементов на действительные (комплексные) числа, т.е. 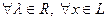определено отображение (обозначение: ), обладающее следующими свойствами:

- ;

- ;

3) Операция сложения элементов и умножения их на числа удовлетворяют законам дистрибутивности:

- ;

- ;

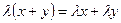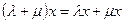Элементы линейного пространства называются векторами. Пространство L называется действительным, если в L операция умножения векторов на число определена только для действительных чисел, и комплексным, если эта операция определена для комплексных чисел.

Примеры линейных пространств:

1) 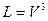– пространство геометрических векторов . :

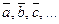- если 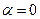, то ;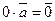

- если 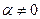, то .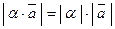

2) 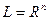– арифметическое пространство.

– множество упорядоченных наборов из n вещественных чисел со следующими правилами:

,

,

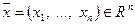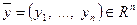
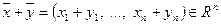
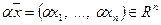3) 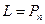– пространство многочленов.

,

,

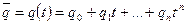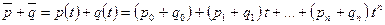
4) – пространство ()-матриц.

(), ()

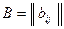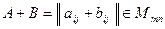
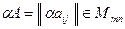
5) 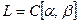– пространство функций, непрерывных на .

,

,

,

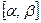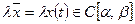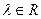
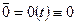Подпространством линейного пространства L называется такое подмножество , которое обладает свойствами:

1) ;

2) .

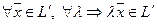Выводы:

1) всякое подпространство содержит ;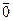

2) каждый вектор в подпространство входит с противоположным.

Теорема 1.

Подпространство линейного пространства само является линейным пространством относительно операций сложения и умножения векторов на число.

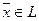является линейной комбинацией векторов системы S, если 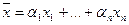, где .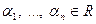

Совокупность линейных комбинаций векторов системы S из линейного пространства L называется линейной оболочкой, т.е.

Теорема 2.

Линейная оболочка 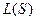системы S в линейном пространстве L образует подпространство в L.

Линейная оболочка системы – наименьшее подпространство, содержащее все векторы системы.

Дата добавления: 2015-04-24