КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример использования статистической меры в семантическом аспекте
|
|
|
|
В качестве случайных событий рассматривается получения сообщений разных по содержанию, каждая из которых имеет свою вероятность. Совокупность возможных сообщений образует ансамбль. Количество полученной информации в данном случае будет равно исчезнувшей у получателя неопределенности.
Например, ансамбль сообщений о результатах экзамена представляет собой следующее множество сообщений
· Отлично, p1 = 1/8
· Хорошо, p2 = 1/4
· Удовлетворительно, p3 = 1/2
· Не удовлетворительно, p4 = 1/8
Количество статистической информации содержащейся в сообщении об отличной оценке, равно
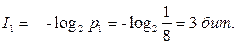
Формула Шеннона является основным утверждением теории информации. Суть, которого следующая – энтропия ансамбля характеризует разнообразие ансамбля. Чем больше энтропия, тем выше степень неопределенности ансамбля.
Свойства энтропии:
1. Характеризует разнообразие ансамбля.
2. Всегда неотрицательно, больше или равна нулю.
3. Энтропия минимальна, если вероятность одного события ансамбля равна единице, а остальных нулю.
4. Энтропия максимальна, когда события ансамбля равновероятны.
В синтаксическом аспекте обобщенная мера информации рассчитывается для использованного в сообщении алфавита и определяет среднее количество информации, содержащееся в одном символе алфавита. Определение энтропии разговорных языков является важной практической задачей, если считать, что все буквы алфавита разговорного языка равновероятны, то энтропия русского и латинского алфавита будет иметь такие значения.
Энтропия алфавитов естественных языков при условии равновероятного выбора букв:
русский алфавит H=loq232=5 бит/букву
латинский алфавит H=loq227=4,75 бит/букву.
Энтропия алфавитов естественных языков при учете вероятности выбора букв:
русский алфавит H=4,35 бит/букву
латинский алфавит H=4,03 бит/букву.
Избыточность алфавитов естественных языков
где Hmax – максимально возможная энтропия алфавита (при равновероятном выборе букв),
H ‑ энтропия алфавита c учетом вероятности выбора букв.
Избыточность русского алфавита – 0,13
Избыточность латинского алфавита – 0,15
Что говорит о большей неравномерности распределения вероятности букв русского алфавита.
В семантическом аспекте обобщенная мера рассчитывается для ансамбля сообщений и определяет среднее количество информации, содержащееся в одном сообщении ансамбля.
| Кодируемый символ | Кодовая комбинация |
Классификация кодов
Код называется равномерным, если все кодовые комбинации его таблицы имеют одинаковую длину, равную длине кода. Длина кода обозначается строчной латинской буквой l.
При равномерном кодировании не требуется разделять кодовые комбинации специальными символами, т.к. в процессе декодирования их можно выделить простым подсчетом символом.
Примером неравномерного кода, является код Морзе, использующий в качестве кодирующего алфавита, алфавит мощностью 2, состоящий из символов «.» и «─». Применяется для кодирования разговорных языков, длина кодовых комбинаций от 1 до 4.
Использование неравномерных кодов позволяет увеличить скорость передачи и обработки информации, однако реализация автоматического декодирования неравномерных кодов довольно сложна, что ограничивает их применение в технике.
Для повышения достоверности сообщения применяют избыточные коды.
В кодовых комбинациях помимо информационных разрядов содержатся проверочные разряды. Которые вводятся для обнаружения и исправления различных ошибок.
В таблицу избыточных кодов включается только определенная часть возможных кодовых комбинаций.
Простой код – код называется простым, если содержит только информационные разряды. Кодовые комбинации отличаются друг от друга хотя бы значениями одного разряда, минимальная длина простого кода с основанием a, обеспечивающая кодирования алфавита мощностью M, определяется следующим соотношением
где N – мощность кодирующего алфавита,
k –натуральное число (k=1, 2, 3,…),
[] – символ целой части.
При выборе кодов предназначенных для преобразования, передачи и хранения данных с помощью технических устройств, производится оценка следующих характеристик кода:
Основание кода – a
Число информационных разрядов кодовых комбинаций – p
Длина кода ‑ l;
Число возможных кодовых комбинаций – N=ql;
Число информационных разрядов в кодовых комбинациях ‑ k;
Мощность кода — Nk=qk;
Абсолютная избыточность кода ‑ r (число проверочных разрядов в кодовой комбинации);
Относительная избыточность кода – 
Чтобы закодировать алфавит мощностью М с использованием избыточного кода необходимо выполнения условия Np≥M
Коды с основанием равным 2 получили название двоичных.
Двоичное кодирование используется в информатике, компьютерной технике и устройствах связи.
Одной из важнейших задач является выбор способа кодирования, обеспечивающая выполнение следующих условий:
- минимальный расход энергии и времени при передачи и обработки сообщений
- минимальное количество ошибок
- максимальные возможности для обнаружения и устранения возникших ошибок.
где Å‑ символ операции сложения по модулю два.
Пример формирования кодовой комбинации Грея
x 3x2x1x0
610=0 1 1 02 –двоичное представление числа
q0=x0 Å x1 =1Å0=1
q1=x1 Å x2 =1Å1=0
q2=x2 Å x3 =0Å1=1
q3=x3 =0
Кодовая комбинация грея: q3 q2 q1 q0 = 0 1 0 1.
таблица кодов Грея
| Десятичное число | Двоичное число | Кодовая комбинация Грея |
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 503; Нарушение авторских прав?; Мы поможем в написании вашей работы!