Определение ранга матрицы

Пример

Пример

Пример

Пример

Пример

Пример

Пример

Пример

Пример

Замечание

Все что будет сказано относительно строк, будет относиться и к столбцам.

1° При транспонировании квадратной матрицы её определитель не меняется: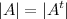

Известно, что определитель матрицы 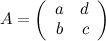равен 3. Тогда определитель матрицы 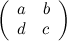, которая равна 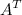, также равен 3.

2° Общий множитель в строке можно выносить за знак определителя.

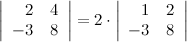
3°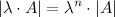

То есть, если квадратная матрица 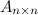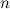-го порядка умножается на некоторое ненулевое число 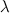, то определитель полученной матрицы равен произведению определителя исходной матрицы 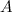на число 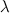в степени, равной порядку матриц.

Задание. Пусть определитель матрицы 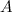третьего порядка равен 3, вычислить определитель матрицы .

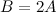Решение. По свойству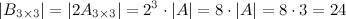

Ответ.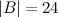

4° Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

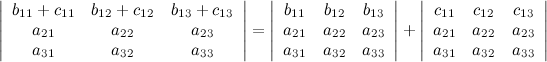
5° Если две строки определителя поменять местами, то определитель поменяет знак.

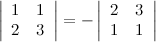
6° Определитель с двумя равными строками равен нулю.

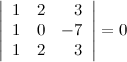
7° Определитель с двумя пропорциональными строками равен нулю.

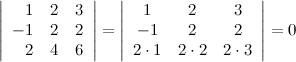
8° Определитель, содержащий нулевую строку, равен нулю.

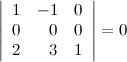
9° Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

Пусть задан определитель третьего порядка 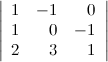. Прибавим ко второй строке определителя третью его строку, при этом значение определителя не измениться:

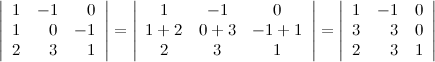
10° Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

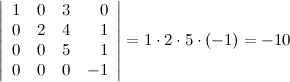
11° Определитель произведения матриц равен произведению определителей: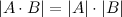

7. Обратная матрица.

Рассмотрим квадратную матрицу

.

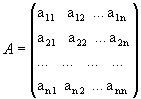Обозначим Δ =det A.

Квадратная матрица А называется невырожденной, или неособенной, если ее определитель отличен от нуля, и вырожденной, или особенной, если Δ = 0.

Квадратная матрица В есть обратная матрица для квадратной матрицы А того же порядка, если их произведение А В = В А = Е, где Е - единичная матрица того же порядка, что и матрицы А и В.

Теорема. Для того, чтобы матрица А имела обратную матрицу, необходимо и достаточно, чтобы ее определитель был отличен от нуля.

Обратная матрица матрице А, обозначается через А^-1, так что В = А^-1 и вычисляется по формуле

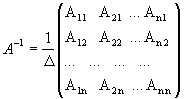, (1)

где А _{i j} - алгебраические дополнения элементов a _{i j} матрицы A..

Вычисление A^-1 по формуле (1) для матриц высокого порядка очень трудоемко, поэтому на практике бывает удобно находить A^-1 с помощью метода элементарных преобразований (ЭП). Любую неособенную матрицу А путем ЭП только столбцов (или только строк) можно привести к единичной матрице Е. Если совершенные над матрицей А ЭП в том же порядке применить к единичной матрице Е, то в результате получится обратная матрица. Удобно совершать ЭП над матрицами А и Е одновременно, записывая обе матрицы рядом через черту. Отметим еще раз, что при отыскании канонического вида матрицы с целью нахождения ранга матрицыможно пользоваться преобразованиями строк и столбцов. Если нужно найти обратную матрицу, в процессе преобразований следует использовать только строки или только столбцы.

8. Ранг матрицы.

Рассмотрим прямоугольную матрицу. Если в этой матрице выделить произвольно k строк и k столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу k-го порядка. Определитель этой матрицы называется минором k-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел m и n. Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен r, то это означает, что в матрице А имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r, равен нулю. Ранг матрицы А обозначается через r(A). Очевидно, что выполняется соотношение

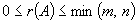
Дата добавления: 2015-04-24