Вычисление ранга матрицы с помощью элементарных преобразований

Элементарными называются следующие преобразования матрицы:

1) перестановка двух любых строк (или столбцов),

2) умножение строки (или столбца) на отличное от нуля число,

3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.

Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: A ~ B.

Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы равны нулю, например,

.

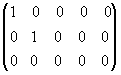При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.

Пример 2 Найти ранг матрицы

А=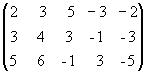

и привести ее к каноническому виду.

Решение. Из второй строки вычтем первую и переставим эти строки:

.

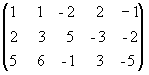Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5:

;

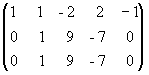из третьей строки вычтем первую; получим матрицу

В = ,

которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и r(A)=2. Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:

.

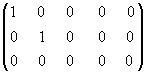9. Системы линейных алгебраических уравнений. Теорема Кронекера-Капелли.

Система линейных алгебраических уравнений с 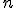неизвестными — это система уравнений вида

Здесь — неизвестные, которые надо определить. Коэффициенты системы 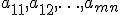и её свободные члены предполагаются известными. Индексы коэффициента 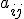системы обозначают номера уравнения 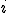и неизвестного 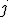, при котором стоит этот коэффициент.

Система называется однородной, если все её свободные члены равны нулю, 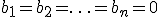, иначе — неоднородной.

Система называется квадратной, если число уравнений равно числу 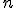неизвестных.

Решение системы уравнений — совокупность 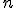чисел 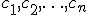, таких что подстановка каждого вместо 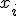в систему обращает все её уравнения в тождества.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у нее нет ни одного решения. Совместная система может иметь одно или более решений.

Решения 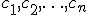и 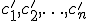совместной системы называются различными, если нарушается хотя бы одно из равенств:

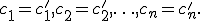
Совместная система называется определенной, если она имеет единственное решение; если же у нее есть хотя бы два различных решения, то она называется неопределенной. Если уравнений больше, чем неизвестных, она называется переопределённой.

Дата добавления: 2015-04-24