
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы решения 1 страница
|
|
|
|
Пример системы линейных уравнений
Матричная форма
Система линейных уравнений может быть представлена в матричной форме как
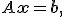
где
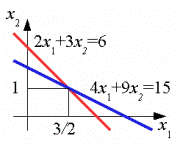

Графическое решение системы линейных уравнений
Система из двух уравнений с двумя неизвестными имеет вид

Чтобы найти неизвестные 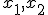 нужно решить верхнее уравнение относительно
нужно решить верхнее уравнение относительно  :
:  а затем подставить полученное решение в нижнее уравнение:
а затем подставить полученное решение в нижнее уравнение: 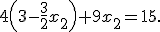 Получено решение
Получено решение  .
.
Данную систему можно наглядно изобразить на графике в виде двух прямых. Точка с координатами  является ее решением.
является ее решением.
Прямые (или точные) методы решения СЛАУ позволяют найти решение за определенное количество шагов. К прямым методам относятся метод Гаусса, метод Гаусса — Жордана, метод Крамера, матричный метод и метод прогонки (для трёхдиагональных матриц).
Итерационные методы основаны на использовании повторяющегося процесса. Они позволяют получить решение в результате последовательных приближений. К итерационным методам относятся метод Якоби (метод простой итерации), метод Гаусса — Зейделя, метод релаксации и многосеточный метод.
| Ранг матрицы. Теорема Кронекера-Капелли |
Определение 1. Пусть имеется матрица размерности  : :
 .
Минором k-го порядка данной матрицы называется определитель, составленный из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы.
Пример. В матрице .
Минором k-го порядка данной матрицы называется определитель, составленный из элементов, стоящих на пересечении произвольно выбранных k строк и k столбцов матрицы.
Пример. В матрице 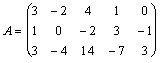 минорами первого порядка являются сами элементы матрицы. Если выбрать две строчки (например, 1-ю и 3-ю) и два столбца (например, 2-й и 5-й), получится минор второго порядка минорами первого порядка являются сами элементы матрицы. Если выбрать две строчки (например, 1-ю и 3-ю) и два столбца (например, 2-й и 5-й), получится минор второго порядка 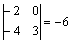 . Если взять три строки и три столбца (например, 1-й, 3-й, и 4-й), получится минор 3-го порядка . Если взять три строки и три столбца (например, 1-й, 3-й, и 4-й), получится минор 3-го порядка
 .
Определение 2. Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров.
Пример. В рассмотренной выше матрице .
Определение 2. Рангом матрицы называется наибольший из порядков отличных от нуля ее миноров.
Пример. В рассмотренной выше матрице  все миноры 3-го порядка равны нулю (это нетрудно проверить, миноров 3-го порядка всего десять), а среди миноров 2-го порядка есть отличные от нуля, например, вычисленный выше. Значит, ранг матрицы все миноры 3-го порядка равны нулю (это нетрудно проверить, миноров 3-го порядка всего десять), а среди миноров 2-го порядка есть отличные от нуля, например, вычисленный выше. Значит, ранг матрицы 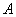 равен двум. Это обозначается: равен двум. Это обозначается:  .
Определение 3. Две матрицы .
Определение 3. Две матрицы 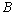 и и 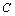 называются эквивалентными (пишут: называются эквивалентными (пишут:  ), если их ранги равны: ), если их ранги равны: 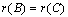 .
Можно показать, что следующие преобразования не меняют ранга матрицы:
1) перестановка строк матрицы;
2) умножение какой-либо строки на действительное число, отличное от нуля;
3) прибавление к элементам одной строки соответствующих элементов другой строки;
4) вычеркивание строки, все элементы которой равны нулю.
Указанные преобразования можно использовать для определения ранга матрицы.
Пример. Для определения ранга матрицы .
Можно показать, что следующие преобразования не меняют ранга матрицы:
1) перестановка строк матрицы;
2) умножение какой-либо строки на действительное число, отличное от нуля;
3) прибавление к элементам одной строки соответствующих элементов другой строки;
4) вычеркивание строки, все элементы которой равны нулю.
Указанные преобразования можно использовать для определения ранга матрицы.
Пример. Для определения ранга матрицы 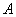 необходимо выполнить цепочку следующих преобразований: необходимо выполнить цепочку следующих преобразований:
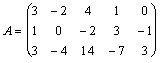 ~ ~ 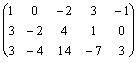 (переставили местами первую и вторую строки) ~ (переставили местами первую и вторую строки) ~  (первую строку умножили на (первую строку умножили на  и сложили со второй; первую строку умножили на и сложили со второй; первую строку умножили на  и сложили с третьей) ~ и сложили с третьей) ~  (элементы третьей строки умножили на (элементы третьей строки умножили на
 ) ~ ) ~ 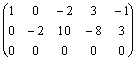 (к элементам третьей строки прибавили элементы второй строки). Преобразованная матрица имеет две ненулевые строки, следовательно, ранг матрицы (к элементам третьей строки прибавили элементы второй строки). Преобразованная матрица имеет две ненулевые строки, следовательно, ранг матрицы 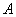 равен двум: равен двум:  .
Определение 4. Пусть дана система .
Определение 4. Пусть дана система 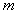 линейных уравнений с линейных уравнений с  неизвестными: неизвестными:
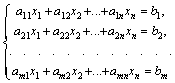 Матрицей системы называют матрицу, составленную из коэффициентов при неизвестных, расширенной матрицей системы – матрицу из коэффициентов с дополнительным столбцом из свободных членов. Если обозначить их соответственно
Матрицей системы называют матрицу, составленную из коэффициентов при неизвестных, расширенной матрицей системы – матрицу из коэффициентов с дополнительным столбцом из свободных членов. Если обозначить их соответственно 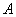 и и  , то , то
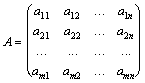 , ,  .
Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы.
Если при этом ранг равен числу неизвестных, то система имеет единственное решение, если он меньше числа неизвестных, решений -множество.
Пример. Исследовать систему линейных уравнений .
Теорема Кронекера-Капелли. Для того чтобы система линейных уравнений была совместна, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы.
Если при этом ранг равен числу неизвестных, то система имеет единственное решение, если он меньше числа неизвестных, решений -множество.
Пример. Исследовать систему линейных уравнений
 Решение. Поскольку все элементы матрицы системы входят в расширенную матрицу, то ранги обеих матриц можно вычислять одновременно.
Решение. Поскольку все элементы матрицы системы входят в расширенную матрицу, то ранги обеих матриц можно вычислять одновременно.
  ~ ~  ~
~ ~
~  .
Таким образом, матрица .
Таким образом, матрица 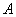 содержит две ненулевые строки, значит ее ранг содержит две ненулевые строки, значит ее ранг 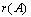 равен двум. В матрице равен двум. В матрице  три ненулевых строки, ее ранг три ненулевых строки, ее ранг 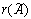 равен трем. А т.к. равен трем. А т.к.  , система несовместна. , система несовместна.
|
10. Матричный способ решения систем линейных уравнений.
Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.
Метод удобен для решения систем невысокого порядка.
Метод основан на применении свойств умножения матриц.
Пусть дана система уравнений:
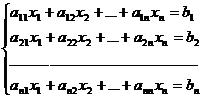
Составим матрицы: A =  ; B =
; B =  ; X =
; X =  .
.
Систему уравнений можно записать:
A*X = B.
Сделаем следующее преобразование: A-1*A*X = A-1*B,
т.к. А-1*А = Е, то Е*Х = А-1*В
Х = А-1*В
Для применения данного метода необходимо находить обратную матрицу, что может быть связано с вычислительными трудностями при решении систем высокого порядка.
11. Формулы Крамера.
Метод Крамера состоит в том, что мы последовательно находим главный определитель системы (5.3), т.е. определитель матрицы А
D = det (ai j)
и n вспомогательных определителей D i (i=  ), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
), которые получаются из определителя D заменой i-го столбца столбцом свободных членов.
Формулы Крамера имеют вид:
D × x i = D i (i =  ). (5.4)
). (5.4)
Из (5.4) следует правило Крамера, которое дает исчерпывающий ответ на вопрос о совместности системы (5.3): если главный определитель системы отличен от нуля, то система имеет единственное решение, определяемое по формулам:
x i = D i / D.
Если главный определитель системы D и все вспомогательные определители D i = 0 (i=  ), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
), то система имеет бесчисленное множество решений. Если главный определитель системы D = 0, а хотя бы один вспомогательный определитель отличен от нуля, то система несовместна.
12. Метод Гаусса.
Пусть исходная система выглядит следующим образом

Матрица 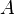 называется основной матрицей системы,
называется основной матрицей системы,  — столбцом свободных членов.
— столбцом свободных членов.
Тогда согласно свойству элементарных преобразований над строками основную матрицу этой системы можно привести к ступенчатому виду (эти же преобразования нужно применять к столбцу свободных членов):

При этом будем считать, что базисный минор (ненулевой минор максимального порядка) основной матрицы находится в верхнем левом углу, то есть в него входят только коэффициенты при переменных  [3].
[3].
Тогда переменные  называются главными переменными. Все остальные называются свободными.
называются главными переменными. Все остальные называются свободными.
Если хотя бы одно число 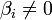 , где
, где 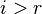 , то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
, то рассматриваемая система несовместна, т.е. у неё нет ни одного решения.
Пусть 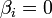 для любых
для любых 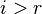 .
.
Перенесём свободные переменные за знаки равенств и поделим каждое из уравнений системы на свой коэффициент при самом левом 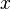 (
(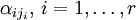 , где
, где 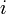 — номер строки):
— номер строки):
 ,
,
где 
Если свободным переменным системы (2) придавать все возможные значения и решать новую систему относительно главных неизвестных снизу вверх (то есть от нижнего уравнения к верхнему), то мы получим все решения этой СЛАУ. Так как эта система получена путём элементарных преобразований над исходной системой (1), то по теореме об эквивалентности при элементарных преобразованиях системы (1) и (2) эквивалентны, то есть множества их решений совпадают.

| Следствия: 1: Если в совместной системе все переменные главные, то такая система является определённой. 2: Если количество переменных в системе превосходит число уравнений, то такая система является либо неопределённой, либо несовместной. |
[править]Условие совместности
Упомянутое выше условие 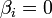 для всех
для всех 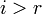 может быть сформулировано в качестве необходимого и достаточного условия совместности:
может быть сформулировано в качестве необходимого и достаточного условия совместности:
Напомним, что рангом совместной системы называется ранг её основной матрицы (либо расширенной, так как они равны)
Определение. Две системы линейных уравнений называются равносильными, если множество всех их решений совпадает.
Определение. Элементарные преобразования системы уравнений — это:
- Вычеркивание из системы тривиальных уравнений, т.е. таких, у которых все коэффициенты равны нулю;
- Умножение любого уравнения на число, отличное от нуля;
- Прибавление к любому i-му уравнению любого j-то уравнения, умноженного на любое число.
Определение. Переменная xi называется свободной, если эта переменная не является разрешенной, а вся система уравнений — является разрешенной.
Теорема. Элементарные преобразования переводят систему уравнений в равносильную.
Смысл метода Гаусса заключается в том, чтобы преобразовать исходную систему уравнений и получить равносильную разрешенную или равносильную несовместную систему.
Итак, метод Гаусса состоит из следующих шагов:
- Рассмотрим первое уравнение. Выберем первый ненулевой коэффициент и разделим все уравнение на него. Получим уравнение, в которое некоторая переменная xi входит с коэффициентом 1;
- Вычтем это уравнение из всех остальных, умножая его на такие числа, чтобы коэффициенты при переменной xi в остальных уравнениях обнулились. Получим систему, разрешенную относительно переменной xi, и равносильную исходной;
- Если возникают тривиальные уравнения (редко, но бывает; например, 0 = 0), вычеркиваем их из системы. В результате уравнений становится на одно меньше;
- Повторяем предыдущие шаги не более n раз, где n — число уравнений в системе.
Каждый раз выбираем для «обработки» новую переменную. Если возникают противоречивые уравнения (например, 0 = 8), система несовместна.
В результате через несколько шагов получим либо разрешенную систему (возможно, со свободными переменными), либо несовместную. Разрешенные системы распадаются на два случая:
Число переменных равно числу уравнений. Значит, система определена;
Число переменных больше числа уравнений. Собираем все свободные переменные справа — получаем формулы для разрешенных переменных. Эти формулы так и записываются в ответ.
13. Системы m линейных уравнений с n переменными, базисные допустимые решения.
Определение 6.1. Базисным решением неопределённой системы линейных уравнений называют такое её решение, в котором все свободные неизвестные равны нулю.
Пример. Исследовать систему линейных уравнений. В случае неопределённости системы найти её базисное решение.

Вычислим ранги основной  и расширенной матриц
и расширенной матриц  данной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:
данной системы уравнений, для чего приведём расширенную (а вместе с тем и основную) матрицу системы к ступенчатому виду:

Вторую строку матрицы сложим с её первой строкой, умноженной на  третью строку – с первой строкой, умноженной на
третью строку – с первой строкой, умноженной на  а четвёртую строку – с первой, умноженной на
а четвёртую строку – с первой, умноженной на 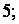 получим матрицу
получим матрицу

К третьей строке этой матрицы прибавим вторую строку, умноженную на 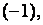 а к четвёртой строке – первую, умноженную на
а к четвёртой строке – первую, умноженную на 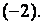 В результате получим матрицу
В результате получим матрицу

удаляя из которой третью и четвёртую строки получим ступенчатую матрицу

Таким образом, 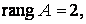
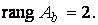 Следовательно, данная система линейных уравнений совместна, а поскольку величина ранга меньше числа неизвестных, система является неопределённой. Полученной в результате элементарных преобразований ступенчатой матрице соответствует система уравнений
Следовательно, данная система линейных уравнений совместна, а поскольку величина ранга меньше числа неизвестных, система является неопределённой. Полученной в результате элементарных преобразований ступенчатой матрице соответствует система уравнений
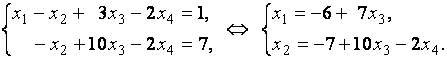
Неизвестные 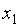 и
и 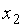 являются главными, а неизвестные
являются главными, а неизвестные  и
и  свободными. Придавая свободным неизвестным нулевые значения, получим базисное решение данной системы линейных уравнений:
свободными. Придавая свободным неизвестным нулевые значения, получим базисное решение данной системы линейных уравнений:

14. Системы линейных однородных уравнений, свойства их решений.
Пусть дана однородная система
 (1)
(1)
Рассмотрим соответствующую неоднородную систему
 (2)
(2)
С помощью матриц
 ,
, 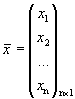 ,
, 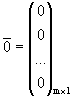 ,
, 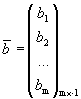
эти системы можно записать в матричном виде.
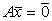 . (3)
. (3)
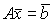 . (4)
. (4)
Справедливы следующие свойства решений однородной и неоднородной систем.
Теорема 1. Линейная комбинация решений однородной системы (1) является решением системы (1).
Доказательство. Пусть 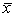 ,
,  и
и 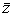 - решения однородной системы (1). Рассмотрим
- решения однородной системы (1). Рассмотрим  , где
, где  ,
,  и
и 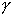 - некоторые произвольные числа. Так как
- некоторые произвольные числа. Так как 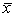 ,
,  и
и 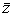 являются решениями, то
являются решениями, то 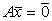 ,
, 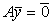 и
и 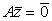 . Найдем
. Найдем 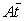 .
.
 .
.
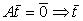 является решением системы (1).
является решением системы (1).
Теорема 2. Разность двух решений неоднородной системы (2) является решением однородной системы (1).
Доказательство. Пусть 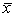 и
и  - решения системы (2). Рассмотрим
- решения системы (2). Рассмотрим 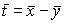 .
.
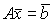 ,
,  .
.
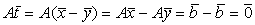 .
.
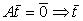 является решением однородной системы (1).
является решением однородной системы (1).
Теорема 3. Сумма решения однородной системы (1) с решением неоднородной системы (8.2) есть решение неоднородной системы (2).
Пусть  - решение системы (1),
- решение системы (1),  - решение системы (2). Покажем, что
- решение системы (2). Покажем, что  - решение системы (2).
- решение системы (2).
Доказательство. 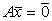 ,
,  .
.
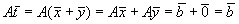 .
.
 является решением неоднородной системы (2).
является решением неоднородной системы (2).
15. Линейные операции над векторами.
Линейными операциями называют операции сложения и вычитания векторов и умножения вектора на число.
Сложение векторов. Пусть 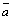 и
и  – два произвольных вектора. Возьмем произвольную точку О и построим вектор
– два произвольных вектора. Возьмем произвольную точку О и построим вектор  ; затем от точки А отложим вектор
; затем от точки А отложим вектор 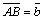 . Вектор
. Вектор 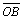 , соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается
, соединяющий начало первого слагаемого вектора с концом второго, называется суммой этих векторов и обозначается  (рис. 1).
(рис. 1).
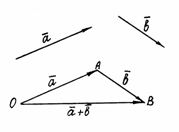
Рис. 1
Ту же сумму можно получить иным способом. Отложим от точки О векторы  и
и  . Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор
. Построим на этих векторах как на сторонах параллелограмм ОАСВ. Вектор  – диагональ параллелограмма – является суммой векторов
– диагональ параллелограмма – является суммой векторов 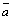 и
и  (рис. 2).
(рис. 2).
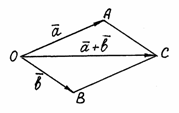
Рис. 2
Понятие суммы можно обобщить на случай любого конечного числа слагаемых (рис. 3).
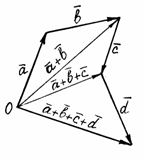
Рис. 3
Вычитание векторов. Разностью 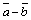 векторов
векторов 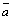 и
и  называется такой вектор
называется такой вектор 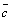 , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор 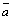 :
: 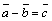 Û
Û  .
.
Если векторы 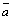 и
и  привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).
привести к общему началу, то разность представляет собой отрезок, соединяющий их концы и направленный от «вычитаемого» к «уменьшаемому» (рис. 4).
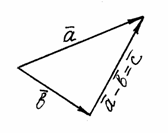
Рис. 4
Таким образом, если на векторах 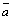 и
и  , отложенных из общей точки О, построить параллелограмм ОАСВ, то вектор
, отложенных из общей точки О, построить параллелограмм ОАСВ, то вектор  , совпадающий с одной диагональю, равен сумме
, совпадающий с одной диагональю, равен сумме  , а вектор
, а вектор  , совпадающий с другой диагональю, – разности
, совпадающий с другой диагональю, – разности 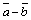 (рис. 5).
(рис. 5).

Рис. 5
Умножение вектора на число. Произведением вектора 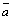 на действительное число
на действительное число  называется вектор
называется вектор  (обозначают
(обозначают 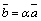 ), определяемый следующими условиями:
), определяемый следующими условиями:
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 501; Нарушение авторских прав?; Мы поможем в написании вашей работы!