Алгоритм шагового метода

Описание шагового метода

Дано уравнение F(x)=0. Задан интервал поиска [x0,x1]. Требуется найти интервал [а,b] длиной h, содержащий первый корень уравнения, начиная с левой границы интервала поиска.

· Установить интервал [а,b] на начало интервала поиска (а=х0).

· Определить координату точки b (b = а + h), а также значения функции в точках а и b: F(a) и F(b).

· Проверить условие F(a)*F(b) < 0. Если условие не выполнено - передвинуть интервал [а,b] на один шаг (а=b) и перейти к пункту 2.

· Если условие выполнено - закончить алгоритм шагового метода.

Решением являются координаты точек а и b. Отрезок [а,b] содержит корень уравнения, поскольку функция F(x) на его концах имеет разные знаки (рис 1).

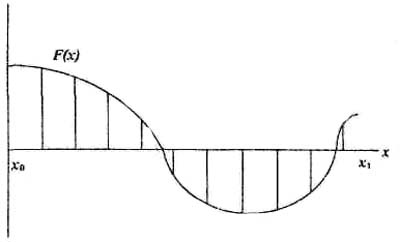
Рис. 1. Иллюстрация шагового метода

Найдя первый корень, можно продолжить поиск корней по тому же алгоритму. В этом случае определяются отрезки, содержащие все корни уравнения на интервале поиска [xO,x1]. Если на всем интервале поиска ни разу не было выполнено условие F(a)*F(b) < 0, то данный интервал вообще не содержит корней. Решение контрольных по математике в контексте нахождения корней уравнения, самый простой способ найти приближенный корень
Достоинство шагового метода: простота алгоритма.
Недостаток метода: для достижения большой точности требуется уменьшать шаг, а это может существенно увеличить время расчета.
Далее используются более точные методы: метод половинного деления или метод Ньютона
Шаговый метод является самым простым и приближенным в решении нелинейных уравнений

3. Основное условие наличия корня нелинейного уравнения в интервале чисел [a,b]:

F(a)*F(b) < 0

4. Если условие наличия корня нелинейного уравнения в заданном интервале чисел [x1,x2] не выполняется ни для одного из более мелких шагов [a,b ]:

передвинуть интервал [а,b] на один шаг (а=b) и перейти к пункту:

· Определить координату точки b (b = а + h), а также значения функции в точках а и b: F(a) и F(b).

· Проверить условие F(a)*F(b) < 0. Если условие не выполнено - передвинуть интервал [а,b] на один шаг (а=b) и перейти к пункту 2.

Если условие выполнено - закончить алгоритм шагового метода.

Сам алгоритм:

· Установить интервал [а,b] на начало интервала поиска (а=х0).

· Определить координату точки b (b = а + h), а также значения функции в точках а и b: F(a) и F(b).

· Проверить условие F(a)*F(b) < 0. Если условие не выполнено - передвинуть интервал [а,b] на один шаг (а=b) и перейти к пункту 2.

· Если условие выполнено - закончить алгоритм шагового метода.

5. Метод половинного деления (дихотомии) для решения нелинейного уравнения основан на:

последовательном сужении интервала, содержащего единственный корень уравнения F(x)=0 до того времени, пока не будет достигнута заданная точность Е

Дата добавления: 2015-04-24