Решение уравнений методом Гаусса

Метод Гаусса самый логичный способ решения уравнений и при решении контрольных по математике результат можно получить достаточно быстро. Метод основан на преобразовании матрицы к треугольному виду. Это достигается последовательным исключением неизвестных из уравнений системы. Сначала с помощью первого уравнения исключается x1 из всех последующих уравнений. Затем с помощью второго уравнения исключается x2 из последующих и т.д. Этот процесс называется прямым ходом метода Гаусса и продолжается до того времени, пока в левой части последнего уравнения не останется только один член с неизвестным х. В результате прямого хода система принимает вид:

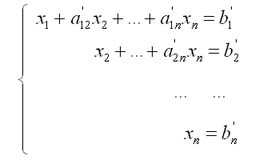
Дальнейшее решение неизвестных метода Гаусса заключается в поочередном нахождении неизвестных, начиная с хn и кончая x1.

Алгоритм прямого хода метода Гаусса:

· Нормируем первое уравнение, разделив его почленно на коэффициент а11.

· Умножаем коэффициенты полученного уравнения на первые коэффициенты остальных уравнений (а21, а31).

· Полученные при перемножении результаты последовательно вычитаем из соответствующих уравнений.

Приведенный алгоритм является наиболее строгой реализацией метода Гаусса и применяется в стандартных программах ЭВМ. На практике можно использовать более простые действия для приведения системы к треугольному виду (переставлять местами уравнения, проводить между ними любые линейные операции).

16. При использовании численных методов решения систем линейных уравнений наибо-лее удобна форма записи системы в виде:

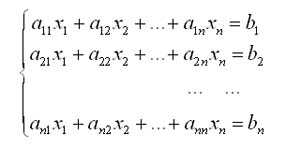
17. При использовании метода простой итерации для решения систем линейных уравнений необходимым начальным приближением корней будет:

необходимо задать начальное приближение вектора неизвестных, в качестве которого обычно выбирается нулевой вектор:

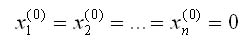
Заметим, что здесь и в дальнейшем нижний индекс обозначает соответствующую компоненту вектора неизвестных, а верхний индекс - номер итерации (приближения).

18. Критерий останова итерационного процесса в методе простой итерации для решения систем линейных уравнений:

Итерационный процесс заканчивается, если для каждой i-й компоненты вектора неизвестных будет выполнено условие достижения точности.
Заметим, что точное решение в методе простой итерации никогда не будет достигнуто, однако с каждой последующей итерацией вектор неизвестных все ближе приближается к точному решению

19. Условие сходимости итерационных методов решения систем линейных уравнений:

Итерационный процесс заканчивается, если для каждой i-й компоненты вектора неизвестных будет выполнено условие достижения точности.
Заметим, что точное решение в методе простой итерации никогда не будет достигнуто, однако с каждой последующей итерацией вектор неизвестных все ближе приближается к точному решению

20. Отличие метода Зейделя от метода простой итерации при решении систем линейных уравнений:

Метод Зейделя (иногда называемый методом Гаусса-Зейделя) является модификацией метода простой итерации, заключающейся в том, что при вычислении очередного приближения x^(k+1) (см. формулы (1.13),(1.14)) его уже полученные компоненты x₁^(k+1),...,x_{i - 1}^(k+1) сразу же используются для вычисления x_i^(k+1).

В координатной форме записи метод Зейделя имеет вид:

x₁^(k+1) = c₁₁x₁^(k) + c₁₂x₂^(k) +... + c_1n-1x_n-1^(k) + c_1nx_n^(k) + d₁
x₂^(k+1) = c₂₁x₁^(k+1) + c₂₂x₂^(k) +... + c_2n-1x_n-1^(k) + c_2nx_n^(k) + d₂
...
x_n^(k+1) = c_n1x₁^(k+1) + c_n2x₂^(k+1) +... + c_nn-1x_n-1^(k+1) + c_nnx_n^(k) + d_n
где x⁽⁰⁾ - некоторое начальное приближение к решению.

Таким образом i -тая компонента (k+1)-го приближения вычисляется по формуле

xi^(k+1) = ∑ j=1^i-1 cijxj^(k+1) + ∑ ^nj=i cijxj^(k) + di, i = 1,..., n

(1.20)

Условие окончания итерационного процесса Зейделя при достижении точности ε в упрощенной форме имеет вид:

|| x ^(k+1) - x ^(k) || ≤ ε.

Существует более точное условие окончания итерационного процесса, которое более сложно и требует дополнительных вычислений

21. Математическая запись векторной модели системы в общем виде:

22. Математическая запись динамической кибернетической модели «черный ящик»:

23. Общепринятая последовательность решения основных системных задач:

24. Тренд временного ряда представляет собой:

25. Интерполяция осуществляется в виде прогноза значений для xi, находящихся по отношению к заданным границам интервала [a,b]:

Интерполя́ция - способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

26. Экстраполяция осуществляется в виде прогноза значений для xi, находящихся по от-ношению к заданным границам интервала [a,b]:

27. Аппроксимация предусматривает условия минимального отклонения значений основ-ной Y(x) и приближающей функций f(x, a0, a1, a2, … am) в интервале [a,b]:

28. Интерполяция предусматривает точное совпадение значений основной Y(x) и прибли-жающей функций f(x, a0, a1, a2, … am) в интервале [a,b]:

29. Линейная интерполяция произвольной функции предусматривает:

Лине́йная интерполя́ция — интерполяция алгебраическим двучленом P1(x) = ax + b функции f, заданной в двух точках x0 и x1 отрезка [a, b]. В случае, если заданы значения в нескольких точках, функция заменяется кусочно-линейной функцией

30. Квадратичная интерполяция произвольной функции предусматривает:

31. Полиномиальная интерполяция произвольной функции предусматривает:

32. Модель прибыли предприятия предусматривает начало выпуска продукции с получе-нием выручки (N) при наличии уровня постоянных затрат (FC):

33. Предприятие с заданными выручкой от продаж (N), уровнем постоянных затрат (FC), общими издержками (затратами Z) начинает давать прибыль (P) при условии:

34. Условие получения максимальной прибыли предприятия при заданной выручке от продаж (N), объемом выпуска продукции (Q), общими издержками (затратами Z):

35. При моделировании условий получения максимальной прибыли предприятия зависи-мость выручки (N) от продажи продукции с объемом выпуска (Q) изделий с заданной це-ной (k) интерполируется:

Дата добавления: 2015-04-24