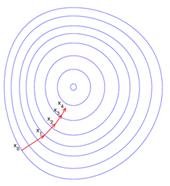
Иллюстрация последовательных приближений к точке экстремума в направлении наискорейшего спуска (красн.) в случае дробного шага. Синим отмечены линии уровня

Описание

Градиентный метод минимизации функции многих переменных.

Градиентный спуск — метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента. Для минимизации функции в направлении градиента используются методы одномерной оптимизации, например, метод золотого сечения. Также можно искать не наилучшую точку в направлении градиента, а какую-либо лучше текущей.

Сходимость метода градиентного спуска зависит от отношения максимального и минимального собственных чисел матрицы Гессе в окрестности минимума (максимума). Чем больше это отношение, тем хуже сходимость метода.

Пусть целевая функция имеет вид:

1. .

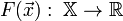2. И задача оптимизации задана следующим образом:

3.

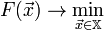
4. Основная идея метода заключается в том, чтобы идти в направлении наискорейшего спуска, а это направление задаётся антиградиентом :

5.

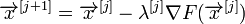
где λ^{[ j ]} выбирается

§ постоянной, в этом случае метод может расходиться;

§ дробным шагом, т.е. длина шага в процессе спуска делится на некое число;

§ наискорейшим спуском: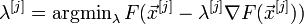

Алгоритм Задают начальное приближение и точность расчёта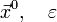

6. Рассчитывают 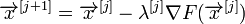, где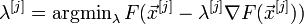

7. Проверяют условие остановки:

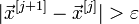§ Если или 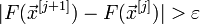(выбирают одно из условий), то j = j + 1 и переход к шагу 2.

§ Иначе 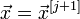и останов.

Дата добавления: 2015-04-24