Линейные операции над векторами

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Билет

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Вопрос

Бюджет маркетинга.

Гибридный

Бинар

Maтрица

Этот план напоминает линейный, однако предполагает ограниченное количество дистрибьюторов на первой линии. Количество людей, которое превзойдет максимально допустимое для первых линий, автоматически перемещается на более низкие уровни. Матричные планы имеют максимально ограниченную глубину и ширину. После того, как все ячейки в матрице заполнены (максимально допустимая глубина и ширина достигнута), открывается новая матрица. Как и в линейных планах, представители матрицы могут получать неограниченные комиссионные на ограниченных товарооборотах, с минимальными требованиями к объемам продаж.

Компенсационный план, который позволяет дистрибьюторам размещать на первой линии только двоих человек. Если дистрибьютор спонсирует более 2-х человек, остальные размещаются ниже первой линии этого спонсора. Этот «спилловер»(spillover) является одной из самых привлекательных черт для новичков, которые должны спонсировать всего 2-х дистрибьюторов, чтобы получать выплаты с маркетинг-плана. Первичное ограничение заключается в том, что для получения комиссионных дистрибьюторы должны «уравновесить» две свои «ноги». Для этого, объем продаж в одной ноге дистрибьютора не должен превышать определенный процент от общего объема его продаж.

Это компенсационный план последнего поколения, составленный из лучших элементов вышеперечисленных планов. Компания Colors Of Life работает с гибридным планом.

Бюджет маркетинга — финансовый план маркетинга, система показателей, раздел плана маркетинга предприятия, в котором в детализированной форме (по элементам комплекса маркетинга или по мероприятиям маркетинга) приведены величины затрат, доходов и прибыли от (для) осуществления маркетинговой деятельности фирмы. Планирование бюджета маркетинга может основываться на целевой прибыли или исходя из оптимизации прибыли.

Составление бюджета маркетинга помогает правильно расставить приоритеты между целями и стратегиями маркетинговой деятельности, принять решения в области распределения ресурсов, осуществлять эффективный контроль.

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины.

Матрицы равны между собой, если равны все их соответствующие элементы.

Матрица, у которой число строк и столбцов равно – называется квадратной.

Матрица, все элементы которой, кроме элементов главной диагонали равны нулю, называется диагональной.

Диагональная матрица, у которой все элементы главной диагонали равны 1, называется единичной. Обозначается буквой Е.

Матрица, у которой все элементы по одну сторону от главной диагонали равны нулю, называется треугольной.

Матрица, у которой все элементы равны нулю, называется нулевой.

1.

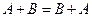
2.

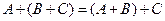
3.

4.

5.

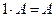
6.

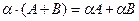
7.

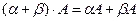
8.

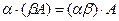
Обратная матрица

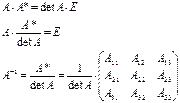
1.

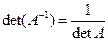
2.

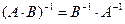
3.

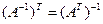
Для того чтобы матрица имела обратную достаточно того, чтобы она была невырождена.

Рангом системы строк (столбцов) матрицы A с m строк и n столбцов называется максимальное число линейно независимых строк (столбцов). Несколько строк (столбцов) называются линейно независимыми, если ни одна из них не выражается линейно через другие. Ранг системы строк всегда равен рангу системы столбцов, и это число называется рангом матрицы

1. Перестановка местами 2 параллельных рядов матрицы.

2. Умножение элементов ряда матрицы на число отличное от нуля, отличное от нуля.

3. Прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.

Из элементов стоящих на пересечении выделенных строк и столбцов, составим определитель k-ого порядка. Наибольший из порядков таких миноров называется рангом матрицы.

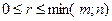
1.

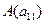
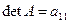
2.

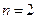
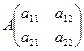
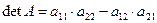
3.

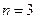
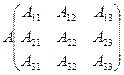
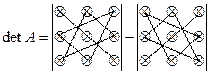
Для нахождения определителя более высокого порядка, матрицу приводят к треугольному виду и считают произведение элементов на главной диагонали.

Свойства определителей

Свойства:

1. Определитель не изменится, если его строки заменить столбцами, и наоборот.

2. При перестановке двух параллельных рядов определитель меняет знак.

3. Определитель, имеющий два одинаковых или пропорциональных ряда, равен нулю.

4. Общий множитель элементов можно вынести за знак определителя.

5. Если элементы какого-либо ряда представляют собой сумму элементов, то определитель может быть разложен на сумму двух соответствующих определителей.

6. Определитель не изменится, если прибавим ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и тоже число.

7. Определитель равен сумме элементов, умноженных на соответствующее им алгебраическое дополнение.

8. Сумма произведения элементов одного ряда на алгебраические дополнения параллельного ряда равна нулю.

СЛУ - это система уравнений вида

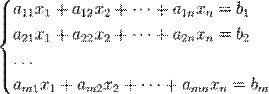
Способы решения систем линейных уравнений делятся на две группы:

1. точные методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, правило Крамера, метод Гаусса и др.),

2. итерационные методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.).

Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если у неё нет ни одного решения.

Совместная система вида (1) может иметь одно или более решений.

Решения c ₁⁽¹⁾, c ₂⁽¹⁾, …, c_n ⁽¹⁾ и c ₁⁽²⁾, c ₂⁽²⁾, …, c_n ⁽²⁾ совместной системы вида (1) называются различными, если нарушается хотя бы одно из равенств:

c ₁⁽¹⁾ = c ₁⁽²⁾, c ₂⁽¹⁾ = c ₂⁽²⁾, …, c_n ⁽¹⁾ = c_n ⁽²⁾.

Совместная система вида (1) называется определённой, если она имеет единственное решение; если же у неё есть хотя бы два различных решения, то она называется неопределённой. Если уравнений больше, чем неизвестных, она называется переопределённой.

Матричная запись системы линейных уравнений
AX = B,где

Матрицу A называют матрицей (или основной матрицей) системы. Матрицу

называют расширенной матрицей системы, а матрицу 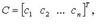для которой AС = В, - вектор-решением системы.

Ма́тричный метод решения (метод решения через обратную матрицу) систем линейных алгебраических уравнений с ненулевым определителем состоит в следующем.

Пусть дана система линейных уравнений с n неизвестными (над произвольным полем):

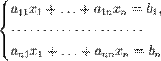
Тогда её можно переписать в матричной форме:

AX = B, где A — основная матрица системы, B и X — столбцы свободных членов и решений системы соответственно:

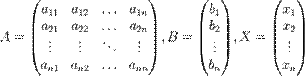
Умножим это матричное уравнение слева на A ^{− 1} — матрицу, обратную к матрице A: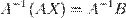

Так как A ^{− 1} A = E, получаем X = A ^{− 1} B. Правая часть этого уравнения даст столбец решений исходной системы. Условием применимости данного метода (как и вообще существования решения неоднородной системы линейных уравнений с числом уравнений, равным числу неизвестных) является невырожденность матрицы A. Необходимым и достаточным условием этого является неравенство нулю определителя матрицы A:

.

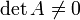Для однородной системы линейных уравнений, то есть когда вектор B = 0, действительно обратное правило: система AX = 0 имеет нетривиальное (то есть ненулевое) решение только если det A = 0. Такая связь между решениями однородных и неоднородных систем линейных уравнений носит название альтернативы Фредгольма.

Метод Гаусса

Сначала следует привести систему к треугольному (ступенчатому) виду, а затем ступенчато решить.

Формула Крамера.

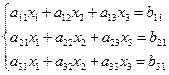
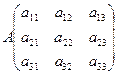
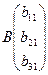
Подсчитать определитель матрицы А.

Затем матрицей B заменить первый столбец матрицы А, подсчитать определитель и разделить его на detA, так мы получим x₁. То же самое проделать со 2-ым и 3-им столбцом.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом. Полярная система координат особенно полезна в случаях, когда отношения между точками проще изобразить в виде радиусов и углов; в более распространённой, декартовой или прямоугольной системе координат, такие отношения можно установить только путём применения тригонометрическихуравнений.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается r) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается 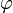, равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.^[1]

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

Векторное уравнение прямой

Положение прямой можно задать по точке и направляющему вектору.

Пусть прямая L задана ее точкой M₀(x₀;y₀;z₀) и направляющим вектором S(m;n;p). Возьмем на прямой L точку M(x;y;z). Обозначим радиус-векторы точек M и M₀ через r и r₀.

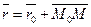
Тогда уравнение прямой запишется в виде: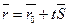

где t – скалярный множитель (параметр).

Канонические уравнения прямой

S(m;n;p) – направляющий вектор прямой L. M₀(x₀;y₀;z₀) – точка на прямой. 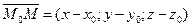соединяет M₀ с произвольной точкой М.

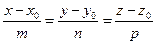
Общее уравнение прямой

Уравнение прямой как линию пересечения двух плоскостей. Рассмотрим:

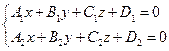
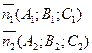
Т.к. прямая перпендикулярна векторам n₁ и n₂ то направляющий вектор запишется как векторное произведение:

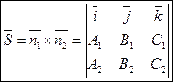
Частные случаи:

1) By + C = 0 - прямая параллельна оси Ox;

2) Ax + C = 0 - прямая параллельна оси Oy;

3) Ax + By = 0 - прямая проходит через начало координат;

4) y = 0 - ось Ox;

5) x = 0 - ось Oy.

Каждый не равный нулю вектор, лежащий на данной прямой или параллельный ей, называется направляющим вектором этой прямой.

Направляющий вектор произвольной прямой в дальнейшем обозначается буквой 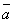, его координаты - буквами l, m, n:

.

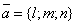Если известна одна точка прямой и направляющий вектор 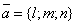, то прямая может быть определена (двумя) уравнениями вида

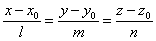. (1)

равнение прямой на плоскости: Ах+Ву+С=0

Координаты нормального вектора: (А;В),

Уравнение прямой с угловым коэффициентом

Если в общем уравнении прямой 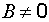, то его можно записать в виде уравнения с угловым коэффициентом

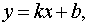
где 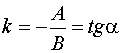угловой коэффициент,

a – угол, образованный прямой с положительным направлением оси 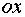, – свободный член, равный ординате точки пересечения прямой с осью .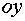

Однозначно определить прямую можно, задав одну точку и угловой коэффициент. А именно, уравнение прямой, проходящей через точку 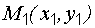с угловым коэффициентом 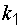, определяется по формуле

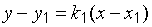. (2)

Пример 1. Составить уравнение прямой проходящей через (.)А(-1,2) с угловым коэффициентом .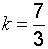

Решение. Воспользуемся формулой (2), подставив координаты данной точки и угловой коэффициент 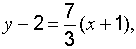или общее уравнение .

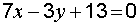Ответ: общее уравнение прямой .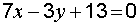

Уравнение прямой в отрезках на прямой

Если в общем уравнении прямой 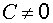, то разделив (1) на 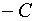, получаем уравнение прямой в отрезках

,

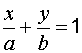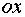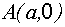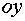где , . Прямая пересекает ось в точке , ось в точке .

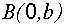Пример 3. Дано общее уравнение прямой 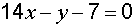. Записать данное уравнение прямой в отрезках.

Решение. , разделим на 7, запишем 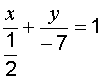. Это уравнение в отрезках. Оно говорит о том, что данная прямая проходит через точки 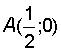, , 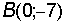т. е. Отсекает на положительной части оси абсцисс , на отрицательной части оси ординат – (-7).

Пример 4. Составить уравнение прямой, отсекающей на осях координат отрезки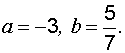

Решение. Уравнение искомой прямой можно записать в отрезках .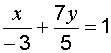

Легко можно привести уравнение к общему виду .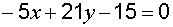

Ответ: .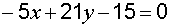

Урав-ние прямой, проход. через данную точку с данным угловым коэффициентом

Уравнение прямой, проходящей через данную точку A (x ₁, y ₁) в данном направлении, определяемом угловым коэффициентом k,

y - y ₁ = k (x - x ₁). (1)

Это уравнение определяет пучок прямых, проходящих через точку A (x ₁, y ₁), которая называется центром пучка.

Урав-ние прямой, проход. через две точки

Уравнение прямой, проходящей через две точки: A (x ₁, y ₁) и B (x ₂, y ₂), записывается так:

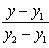
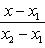
(2)

Угловой коэффициент прямой, проходящей через две данные точки, определяется по формуле

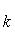
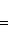
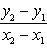
(3)

Определение. Если заданы две прямые y = k₁ x + b₁, y = k ₂x + b₂, то острый угол между этими прямыми будет определяться как

.

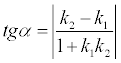Две прямые параллельны, если k₁ = k₂.

Две прямые перпендикулярны, если k₁ = -1/ k₂.

Теорема. Прямые Ах + Ву + С = 0 и А ₁ х + В₁ у + С₁ = 0 параллельны, когда пропорциональны коэффициенты А₁ = λА, В₁ = λВ. Если еще и С₁ = λС, то прямые совпадают.

Координаты точки пересечения двух прямых находятся как решение системы уравнений этих прямых.

Взаимное расположение двух прямых на плоскости

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k ₁ = k ₂. (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

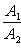
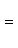
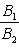
(9)

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

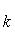
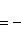
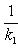
(10)

Это условие может быть записано также в виде

k ₁ k ₂ = -1. (11)

б) Если уравнения прямых заданы в общем виде (6), то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A ₁ A ₂ + B ₁ B ₂ = 0. (12)

Координаты точки пересечения двух прямых находят, решая систему уравнений (6). Прямые (6) пересекаются в том и только в том случае, когда

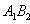
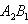
Расстояние от точки до прямой

Теорема. Если задана точка М(х₀, у₀), то расстояние до прямой Ах + Ву + С =0 определяется как

.

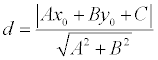Доказательство. Пусть точка М ₁(х ₁, у ₁) – основание перпендикуляра, опущенного из точки М на заданную прямую. Тогда расстояние между точками М и М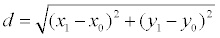₁:

(1)

Координаты x₁ и у₁ могут быть найдены как решение системы уравнений:

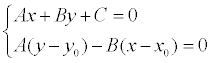
Второе уравнение системы – это уравнение прямой, проходящей через заданную точку М ₀ перпендикулярно заданной прямой.

Если преобразовать первое уравнение системы к виду:

A(x – x ₀) + B(y – y₀) + Ax₀ + By₀ + C = 0,

то, решая, получим:

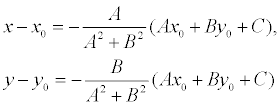
Подставляя эти выражения в уравнение (1), находим:

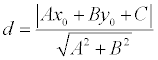
Теорема доказана.

Пример. Определить угол между прямыми: y = -3 x + 7; y = 2 x + 1.

k ₁ = -3; k ₂ = 2; tgφ = 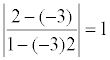; φ= p /4.

Пример. Показать, что прямые 3х – 5у + 7 = 0 и 10х + 6у – 3 = 0 перпендикулярны.

Находим: k ₁ = 3/5, k₂ = -5/3, k 1* k 2 = -1, следовательно, прямые перпендикулярны.

Пример. Даны вершины треугольника А(0; 1), B (6; 5), C (12; -1). Найти уравнение высоты, проведенной из вершины С.

Находим уравнение стороны АВ: 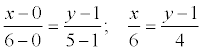; 4 x = 6 y – 6;

2 x – 3 y + 3 = 0;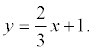

Искомое уравнение высоты имеет вид: Ax + By + C = 0 или y = kx + b.

k = 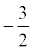. Тогда y = 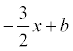. Т.к. высота проходит через точку С, то ее координаты удовлетворяют данному уравнению: 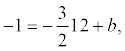откуда b = 17. Итого:.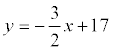

Ответ: 3 x + 2 y – 34 = 0.

Окружность

Окружностью (рис.1) называется геометрическое место точек, равноудалённых от данной точки О, называемой центром окружности, на расстояние R. Число R > 0 называется радиусом окружности.

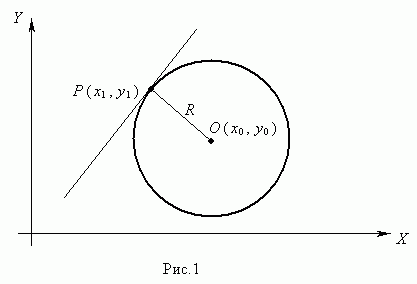
Уравнение окружности радиуса R с центром в точке О (х ₀, у ₀) имеет вид:

(х – х ₀ ) ² + (у – у ₀ ) ² = R ².

Если центр окружности совпадает с началом координат, то уравнение окружности упрощается:

х ² + у ² = R ².

Пусть Р (х ₁, у ₁) – точка окружности (рис.1), тогда уравнение касательной к окружности в данной точке имеет вид:

(х ₁ – х ₀ ) (х – х ₀ ) + (у ₁ – у ₀ ) (у – у ₀ ) = R ².

Условие касания прямой y = m x + k и окружности х ² + у ² = R ²:

k ² / (1 + m ² )= R ².

Эллипс

Эллипсом (рис.1) называется геометрическое место точек, сумма расстояний от которых до двух заданных точек F ₁ и F ₂ , называемых фокусами эллипса, есть величина постоянная.

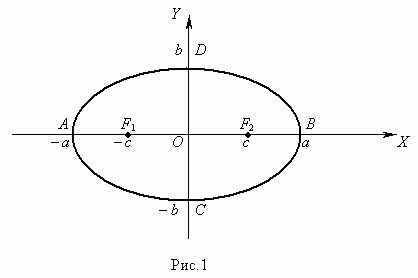
Уравнение эллипса (рис.1):

Здесь начало координат является центром симметрии эллипса, а оси координат – его осями симметрии. При a > b фокусы эллипса лежат на оси ОХ (рис.1), при a < b фокусы эллипса лежат на оси ОY, а при a = b эллипс становится окружностью (фокусы эллипса в этом случае совпадают с центром окружности). Таким образом, окружность есть частный случай эллипса.

Отрезок F ₁ F ₂ = 2 с, где 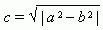, называется фокусным расстоянием. Отрезок AB = 2 a называется большой осью эллипса, а отрезок CD = 2 b – малой осьюэллипса. Число e = c / a, e < 1 называется эксцентриситетом эллипса.

Пусть Р (х ₁, у ₁) – точка эллипса, тогда уравнение касательной к эллипсу в данной точке имеет вид:

Условие касания прямой y = m x + k и эллипса х ² / a ² + у ² / b ² = 1:

k ² = m ² a ²+ b ².

Гипербола

Гиперболой (рис.1) называется геометрическое место точек, модуль разности расстояний от которых до двух заданных точек F ₁ и F ₂ , называемых фокусами гиперболы, есть величина постоянная.

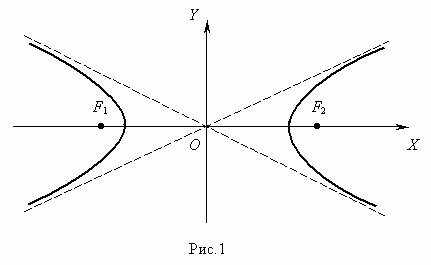
Уравнение гиперболы (рис.1):

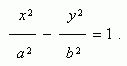
Здесь начало координат является центром симметрии гиперболы, а оси координат – её осями симметрии.

Отрезок F ₁ F ₂ = 2 с, где 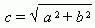, называется фокусным расстоянием. Отрезок AB = 2 a называется действительной осью гиперболы, а отрезок CD = 2 b – мнимой осьюгиперболы. Число e = c / a, e > 1 называется эксцентриситетомгиперболы. Прямые y = ± (b / a) x называются асимптотами гиперболы.

Пусть Р (х ₁, у ₁) – точка гиперболы, тогда уравнение касательной к гиперболе в данной точке имеет вид:

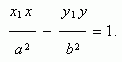
Условие касания прямой y = m x + k и гиперболы х ² / a ² – у ² / b ² = 1:

k ² = m ² a ²– b ².

Парабола

Парабола (рис. 4.16)

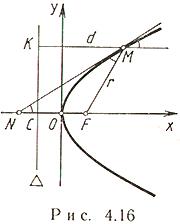
Пусть на плоскости заданы точка F и прямая , не проходящая через F. Парабола - множество всех тех точек M плоскости, каждая из которых равноудалена от точки F и прямой . Точка F называется фокусом, прямая - директрисой параболы; (OF) - ось, O - вершина, 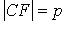- параметр, 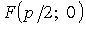- фокус, - фокальный радиус.

Каноническое уравнение: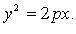

Эксцентриситет: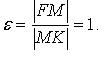

Фокальный радиус: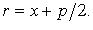

Уравнение директрисы: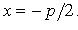

Уравнение касательной в точке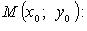

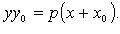
Свойство касательной к параболе: 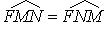(М - точка касания; N - точка пересечения касательной с осью Ox).

Уравнение нормали в точке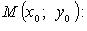

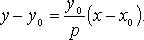
Уравнение диаметра, сопряженного хордам с угловым коэффициентом k: y = p/k.

Параметрические уравнения параболы: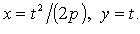

Полярное уравнение: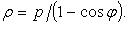

Векторы в пространстве

Вектор - это направленный прямолинейный отрезок, т. е. отрезок, имеющий определенную длину и определенное направление. Если А — начало вектора, а В - его конец, то вектор обозначается символом АВ или а. Вектор ВА (у него начало в точке В, а конец в точке A) называется противоположным вектору АВ. Вектор, противоположный вектору а, обозначается - а.

Длиной или модулем вектора АВ называется длина отрезка и обозначается |АВ|. Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 0. Нулевой вектор направления не имеет.

Вектор, длина которого равна единице, называется единичным вектором и обозначается через e. Единичный вектор, направление которого совпадает с направлением вектора a, называется ортом вектора a и обо значается a °.

Векторы а и b называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают a ||b.

Коллинеарные векторы могут быть направлены одинаково или противоположно.

Нулевой вектор считается коллинеарным любому вектору.

Два вектор а и b называются равными (а = b), если они коллинеарны, одинаково направлены и имеют одинаковые длины.

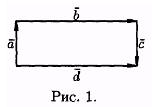
Из определения равенства векторов следует, что вектор можно переносить параллельно самому себе, а начало вектора помещать в любую точку О пространства.

На рисунке 1 векторы образуют прямоугольник. Справедливо равенство b =d, но а¹ с. Векторы а и с — противоположные, а =-с.

Равные векторы называют также свободными.

Три вектора в пространстве называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях. Если среди трех векторов хотя бы один нулевой или два любые коллинеарны, то такие векторы компланарны

Под линейными операциями над векторами понимают операции сложения и вычитания векторов, а также умножение вектора на число.

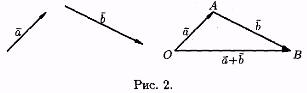
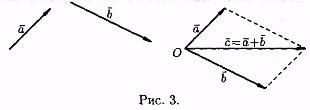
Пусть а и b — два произвольных вектора. Возьмем произвольную точку О и построим вектор ОА=а. От точки А отложим вектор АВ = b. Вектор ОВ, соединяющий начало первого вектора с концом второго, называется суммой векторов а и b: О B=а+b (см. рис. 2)

.

Это правило сложения векторов называют правилом треугольника. Сумму двух векторов можно построить также по правилу параллелoграмма (см. рис. 3).

На рисунке 4 показано сложение трех векторов а, b и с.

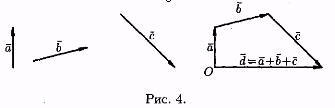
Под разностью векторов а и b понимается вектор с=а-b такой, что b+с=а (см. рис. 5).

Отметим, что в параллелограмме, построенном на векторах а и b одна направленная диагональ является суммой векторов а и b, адругая — разностью (см. рис. 6).

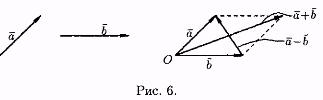
Можно вычитать векторы по правилу: а - b = а + (-b), т. е. вычитание векторов заменить сложением вектора а с вектором, противоположным вектору b.

Произведением вектора а на скаляр (число) λ называется вектор λ*а (или а*λ), который имеет длину |λ|*|а|, коллинеарен вектору а, имеет направление вектора а, если λ>0 и противоположное направление, если λ<0. Из определения произведения вектора на число следуют свойства этого произведения:

1) если b=λ * а, то b|| а. Наоборот, если b || а, ( а¹0), то при некотором λ верно равенство b = λа;

2) всегда а =|а | • а ^-о, т. е. каждый вектор равен произведению его мо дуля на орт.

Линейные операции над векторами обладают следующими свойствами:

1. а+b=b+а
2. (а +b) +с=а + (b +с),
3. λ1 • (λ2 •а) =λ1 •λ2 •а,
4. (λ1 +λ2) •а =λ1 •а +λ2 •а,
5. λ • (а +b) =λ •а+λ •b.

Эти свойства позволяют проводить преобразования в линейных операциях с вектором так, как это делается в обычной алгебре: слагаемые менять местами, вводить скобки, группировать, выносить за скобки как скалярные, так и векторные общие множители.

Дата добавления: 2015-04-24