
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Условие параллельности двух плоскостей
|
|
|
|
Вопрос
Вопрос
Вопрос
Вопрос
Вопрос
Вопрос
Скалярное произведение векторов и свойства
Скалярным произведением векторов 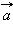 и
и  называется произведение их длин на косинус угла между ними:
называется произведение их длин на косинус угла между ними:
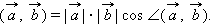
|
Совершенно аналогично, как в планиметрии, доказываются следующие утверждения:
· Скалярное произведение двух ненулевых векторов равно нулю тогда и только тогда, когда эти векторы перпендикулярны.
· Скалярный квадрат вектора, то есть скалярное произведение его самого на себя, равно квадрату его длины.
· Скалярное произведение двух векторов 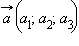 и
и  заданных своими координатами, может быть вычислено по формуле
заданных своими координатами, может быть вычислено по формуле 
Перечислим основные свойства скалярного произведения, которые также доказываются аналогично планиметрическим.
Для любых векторов 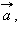
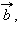 и
и 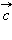 и любого числа λ справедливы равенства:
и любого числа λ справедливы равенства:
1. 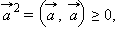 причем
причем 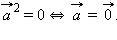
2. 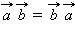 (переместительный закон).
(переместительный закон).
3. 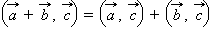 (распределительный закон).
(распределительный закон).
4.  (сочетательный закон).
(сочетательный закон).
Векторное произведение векторов и их свойства
Три некомпланарных вектора образуют правую тройку если с конца третьего поворот от первого вектора ко второму совершается против часовой стрелки. Если по часовой – то левую. Векторным произведением вектора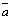 на вектор
на вектор  называется вектор
называется вектор 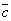 , который:1. Перпендикулярен векторам
, который:1. Перпендикулярен векторам 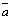 и
и  .2. Имеет длину, численно равную площади параллелограмма, образованного навекторах
.2. Имеет длину, численно равную площади параллелограмма, образованного навекторах 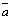 и
и  .
. 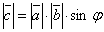 , где
, где 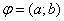 3. Векторы
3. Векторы 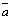 ,
,  и
и 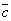 образуют правую тройку векторов. Свойства: 1.
образуют правую тройку векторов. Свойства: 1. 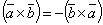 2.
2.  3.
3. 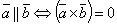 4.
4. 
Смешанное произведение векторов и их свойства
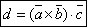 .Смысл смешенного произведения: сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором. Смешанное произведение представляет собой число – число. Результат смешанного произведения – объем параллелепипеда, образованного векторами. Свойства. 1. Смешанное произведение не меняется при циклической перестановкесомножителей:
.Смысл смешенного произведения: сначала два вектора векторно перемножают, а затем полученный скалярно перемножают с третьим вектором. Смешанное произведение представляет собой число – число. Результат смешанного произведения – объем параллелепипеда, образованного векторами. Свойства. 1. Смешанное произведение не меняется при циклической перестановкесомножителей: 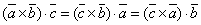 2. Смешанное произведение не изменится при перемене местами векторного искалярного произведения.
2. Смешанное произведение не изменится при перемене местами векторного искалярного произведения. 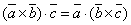 3. Смешанное произведение меняет знак при перемене мест любых двухвекторов-сомножителей.
3. Смешанное произведение меняет знак при перемене мест любых двухвекторов-сомножителей. 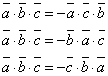 4. Смешанное произведение трех ненулевых векторов равно нулю тогда итолько тогда, когда они компланарны.
4. Смешанное произведение трех ненулевых векторов равно нулю тогда итолько тогда, когда они компланарны. 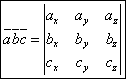 Три вектора называются компланарными, если результат смешанного произведенияравен нулю.
Три вектора называются компланарными, если результат смешанного произведенияравен нулю. Общее уравнение плоскости
Расстояние от точки до плоскости
Расстояние от точки до плоскости --- это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость. Если плоскость задана уравнением 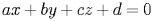 , то расстояние
, то расстояние 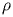 от точки
от точки  до этой плоскости можно вычислить по формуле
до этой плоскости можно вычислить по формуле
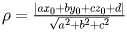
Угол между плоскостями
 Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
Рассмотрим две плоскости α1 и α2, заданные соответственно уравнениями:
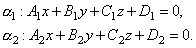
Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами 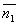 и
и  плоскостей α1 и α2 равен одному из указанных смежных двугранных углов
плоскостей α1 и α2 равен одному из указанных смежных двугранных углов  или
или 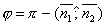 . Поэтому
. Поэтому  . Т.к.
. Т.к. 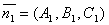 и
и 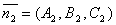 , то
, то
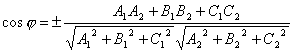 .
.
Пример. Определить угол между плоскостями x +2 y -3 z +4=0 и 2 x +3 y + z +8=0.
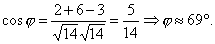
Две плоскости α1 и α2 параллельны тогда и только тогда, когда их нормальные векторы 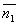 и
и  параллельны, а значит
параллельны, а значит  .
.
Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:
 или
или 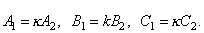
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 432; Нарушение авторских прав?; Мы поможем в написании вашей работы!