
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е
|
|
|
|
Вопрос
Вопрос
Вопрос
Предел функции в точке
Число  называется пределом функции
называется пределом функции 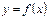 при
при  стремящемся к
стремящемся к 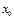 (или в точке
(или в точке 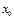 ), если для любого, даже сколько угодно малого положительного числа
), если для любого, даже сколько угодно малого положительного числа 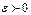 , найдется такое положительное число
, найдется такое положительное число  (зависящее от
(зависящее от 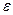 ), что для всех
), что для всех  , не равных
, не равных 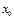 и удовлетворяющих условию
и удовлетворяющих условию 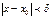 , выполняется неравенство
, выполняется неравенство 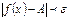 .
.
Это предел функции обозначается:  или
или 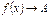 при
при  .
.
Если при стремлении  к
к 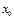 переменная
переменная  принимает лишь значения, меньшие
принимает лишь значения, меньшие 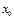 , или наоборот, лишь значения большие
, или наоборот, лишь значения большие 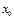 , и при этом функция
, и при этом функция  стремится к некоторому числу
стремится к некоторому числу  , то говорят об односторонних пределах функции
, то говорят об односторонних пределах функции  соответственно слева
соответственно слева 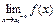 и справа
и справа  .
.
Признаки существования предела
Теорема 1. Если числовая последовательность 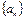 монотонна и ограничена, то она имеет предел.
монотонна и ограничена, то она имеет предел.
Теорема 2. Если в некоторой окрестности точки 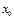 (или при достаточно больших значениях
(или при достаточно больших значениях  ) функция
) функция  заключена между двумя функциями
заключена между двумя функциями 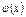 и
и 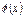 , имеющими одинаковый предел
, имеющими одинаковый предел  при
при  (или
(или  ), то функция
), то функция  имеет тот же предел
имеет тот же предел  .
.
Пусть при 
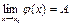 ,
,  .
.
Это означает, что для любого 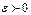 найдется такое число
найдется такое число  , что для всех
, что для всех  и удовлетворяющих условию
и удовлетворяющих условию 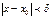 будут верны одновременно неравенства:
будут верны одновременно неравенства:
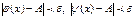 (1.1)
(1.1)
или
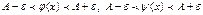
Т.к. по условию функция  заключена между двумя функциями, т.е.:
заключена между двумя функциями, т.е.:
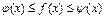 , то из неравенств (1.1) следует, что
, то из неравенств (1.1) следует, что 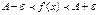 , т.е.:
, т.е.:
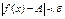 .
.
А это и означает, что 
Бесконечно малые и большие функции и их свойства
Бесконечно малые величины
Определение. Функция  называется бесконечно малой величиной при
называется бесконечно малой величиной при 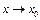 или при
или при 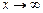 , если ее предел равен нулю:
, если ее предел равен нулю:
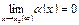 .
.
Связь бесконечно малых величин с пределами функций
Теорема 1. Если функция  имеет при
имеет при 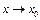 (
(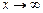 ) предел, равный
) предел, равный 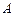 , то ее можно представить в виде суммы этого числа
, то ее можно представить в виде суммы этого числа 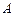 и бесконечно малой
и бесконечно малой  при
при 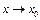 (
(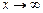 ), т.е.
), т.е.
 .
.
Теорема 2. Если функцию  можно представить как сумму числа
можно представить как сумму числа 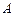 и бесконечно малой
и бесконечно малой  при
при 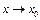 (
(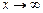 ), то число
), то число 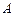 есть предел этой функции при
есть предел этой функции при 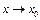 (
(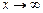 ), т.е.
), т.е.
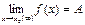 .
.
Свойства бесконечно малых величин
1) Алгебраическая сумма конечного числа бесконечного малых величин есть величина бесконечно малая.
По условию 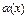 и
и  - бесконечно малые величины при
- бесконечно малые величины при 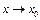 . Это означает, что для любого
. Это означает, что для любого  найдутся такие числа
найдутся такие числа 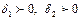 , что для всех
, что для всех  и удовлетворяющих условиям:
и удовлетворяющих условиям:
 и
и  (1.1)
(1.1)
выполняются соответствующие неравенства:
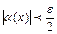 и
и  . (1.2)
. (1.2)
Если взять в качестве числа 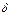 минимальное из чисел
минимальное из чисел 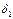 и
и 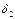 , т.е.
, т.е. 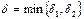 , то неравенству
, то неравенству 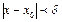 будут удовлетворять решения обоих неравенств (1.1), а, следовательно, одновременно будут верны неравенства (1.2). Складывая почленно неравенства (1.2), получим, что;
будут удовлетворять решения обоих неравенств (1.1), а, следовательно, одновременно будут верны неравенства (1.2). Складывая почленно неравенства (1.2), получим, что;
 .
.
Используя свойство абсолютных величин, т.е.  , придем к более сильному неравенству:
, придем к более сильному неравенству:
 (1.3)
(1.3)
Итак, для любого 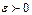 существует такое
существует такое 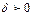 , что для всех
, что для всех  и удовлетворяющих условию
и удовлетворяющих условию 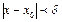 верно неравенство (1.3). А это означает, что функция
верно неравенство (1.3). А это означает, что функция 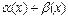 есть величина бесконечно малая.
есть величина бесконечно малая.
2) Произведение бесконечно малой величины на ограниченную функцию (в т.ч. на постоянную, на другую бесконечно малую) есть величина бесконечно малая.
3) Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Отношение двух бесконечно малых (неопределенность вида  ) в зависимости от характера изменения переменных в числителе и знаменателе может оказаться или числом, или бесконечно малой или бесконечностью.
) в зависимости от характера изменения переменных в числителе и знаменателе может оказаться или числом, или бесконечно малой или бесконечностью.
Бесконечно большие величины
Определение. Функция  называется бесконечно большой при
называется бесконечно большой при  , если ее предел равен бесконечности:
, если ее предел равен бесконечности:
 .
.
Свойства бесконечно больших величин
1) Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
2) Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
3) Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.
Об отношении или разности двух бесконечно больших функций никакого общего заключения сделать нельзя. В этих случаях говорят о неопределенностях вида  или
или  . В зависимости от характера изменения бесконечно больших величин их отношение или разность может оказаться или числом, или бесконечно малой, или бесконечно большой.
. В зависимости от характера изменения бесконечно больших величин их отношение или разность может оказаться или числом, или бесконечно малой, или бесконечно большой.
Связь между бесконечно малыми и бесконечно большими величинами
Теорема. Если функция  есть бесконечно малая величина при
есть бесконечно малая величина при  (
(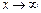 ), то функция
), то функция 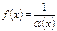 является бесконечно большой при
является бесконечно большой при  (
(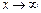 ). И, наоборот, если функция
). И, наоборот, если функция  бесконечно большая при
бесконечно большая при  (
(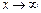 ), то функция
), то функция 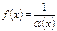 есть величина бесконечно малая при
есть величина бесконечно малая при  (
(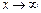 ).
).
Теоремы о пределах
Сформулируем основные теоремы о пределах:
1) Функция не может иметь более одного предела.
Предположим противное, т.е. что функция  имеет 2 предела А и D,
имеет 2 предела А и D,  . Тогда на основании теоремы о связи бесконечно малых величин с пределами функции:
. Тогда на основании теоремы о связи бесконечно малых величин с пределами функции: 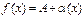 ,
,  , где
, где 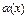 и
и 
 - бесконечно малые величины при
- бесконечно малые величины при  (
( ). Вычитая почленно эти равенства, получим:
). Вычитая почленно эти равенства, получим:  , откуда
, откуда  . Это равенство невозможно, т.к. на основании свойства 1 бесконечно малых
. Это равенство невозможно, т.к. на основании свойства 1 бесконечно малых  это величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно.
это величина бесконечно малая. Следовательно, предположение о существовании второго предела неверно.
2) Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е.
 .
.
3) Предел произведения конечного числа функций равен произведению пределов этих функций, т.е.
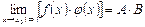 .
.
По условию  и
и  , следовательно, на основании теоремы о связи бесконечно малых величин с пределами функции:
, следовательно, на основании теоремы о связи бесконечно малых величин с пределами функции: 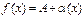 ,
,  , где
, где 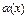 и
и  - бесконечно малые величины при
- бесконечно малые величины при  (
( ). Перемножая почленно оба равенства, получим:
). Перемножая почленно оба равенства, получим:
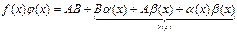 .
.
На основании свойств бесконечно малых последние три слагаемые представляют величину, бесконечно малую 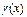 при
при  (
( ).
).
Итак, функция  представляет сумму постоянного числа
представляет сумму постоянного числа  и бесконечного малой
и бесконечного малой 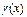 . На основании обратной теоремы о связи бесконечно малых с пределами функции это означает, что
. На основании обратной теоремы о связи бесконечно малых с пределами функции это означает, что  .
.
В частности, постоянный множитель можно выносить за знак предела, т.е.
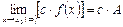 .
.
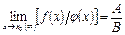 ,
,  .
.
5) Если 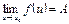 ,
, 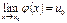 , то предел сложной функции
, то предел сложной функции
 .
.
6) Если в некоторой окрестности точки 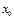 (или при достаточно больших
(или при достаточно больших  )
)  , то
, то
 .
.
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1228; Нарушение авторских прав?; Мы поможем в написании вашей работы!