
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример. Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х
|
|
|
|
Вопрос
Вопрос
Вопрос
Вопрос
График функции
Выберем на плоскости прямоугольную систему координат и будем откладывать на оси абсцисс значения аргумента х, а на оси ординат - значения функции у = f (х).
Графиком функции y = f(x) называется множество всех точек, у которых абсциссы принадлежат области определения функции, а ординаты равны соответствующим значениям функции.
Другими словами, график функции y = f (х) - это множество всех точек плоскости, координаты х, у которых удовлетворяют соотношению y = f(x).
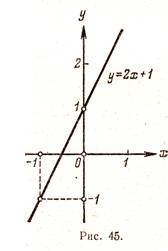
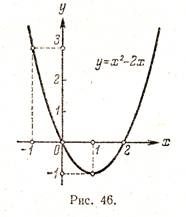
На рис. 45 и 46 приведены графики функций у = 2х + 1 и у = х2 — 2х.
Строго говоря, следует различать график функции (точное математическое определение которого было дано выше) и начерченную кривую, которая всегда дает лишь более или менее точный эскиз графика (да и то, как правило, не всего графика, а лишь его части, расположенного в конечной части плоскости). В дальнейшем, однако, мы обычно будем говорить «график», а не «эскиз графика».
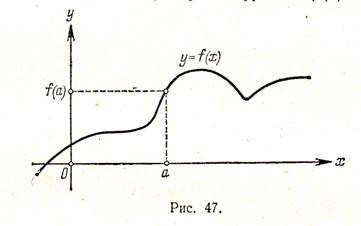
С помощью графика можно находить значение функции в точке. Именно, если точка х = а принадлежит области определения функции y = f(x), то для нахождения числа f(а) (т. е. значения функции в точке х = а) следует поступить так. Нужно через точку с абсциссой х = а провести прямую, параллельную оси ординат; эта прямая пересечет график функции y = f(x) в одной точке; ордината этой точки и будет, в силу определения графика, равна f(а) (рис. 47).
Например, для функции f(х) = х2 — 2x с помощью графика (рис. 46) находим f(-1) = 3, f(0) = 0, f(1) = -l, f(2) = 0 и т. д.
График функции наглядно иллюстрирует поведение и свойства функции. Например, из рассмотрения рис. 46 ясно, что функция у = х2— 2х принимает положительные значения при х < 0 и при х > 2, отрицательные - при 0 < x < 2; наименьшее значение функция у = х2 - 2х принимает при х = 1.
Для построения графика функции f(x) нужно найти все точки плоскости, координаты х, у которых удовлетворяют уравнению y = f(x). В большинстве случаев это сделать невозможно, так как таких точек бесконечно много. Поэтому график функции изображают приблизительно - с большей или меньшей точностью. Самым простым является метод построения графика по нескольким точкам. Он состоит в том, что аргументу х придают конечное число значений - скажем, х1, х2, x3,..., хk и составляют таблицу, в которую входят выбранные значения функции.
Таблица выглядит следующим образом:
| x | x1 | x2 | x3 | ... | xk |
| y | f(x1) | f(x2) | f(x3) | ... | f(xk) |
Составив такую таблицу, мы можем наметить несколько точек графика функции y = f(x). Затем, соединяя эти точки плавной линией, мы и получаем приблизительный вид графика функции y = f(x).
Следует, однако, заметить, что метод построения графика по нескольким точкам очень ненадежен. В самом деле поведение графика между намеченными точками и поведение его вне отрезка между крайними из взятых точек остается неизвестным.
Пример 1. Для построения графика функции y = f(x) некто составил таблицу значений аргумента и функции:
| x | -2 | -1 | |||
| y | -1 |
Соответствующие пять точек показаны на рис. 48.
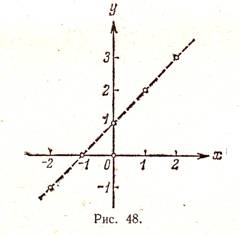
На основании расположения этих точек он сделал вывод, что график функции представляет собой прямую (показанную на рис. 48 пунктиром). Можно ли считать этот вывод надежным? Если нет дополнительных соображений, подтверждающих этот вывод, его вряд ли можно считать надежным. надежным.
Для обоснования своего утверждения рассмотрим функцию
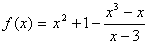 .
.
Вычисления показывают, что значения этой функции в точках -2, -1, 0, 1, 2 как раз описываются приведенной выше таблицей. Однако график этой функции вовсе не является прямой линией (он показан на рис. 49). Другим примером может служить функция y = x + l + sinπx; ее значения тоже описываются приведенной выше таблицей.
Эти примеры показывают, что в «чистом» виде метод построения графика по нескольким точкам ненадежен. Поэтому для построения графика заданной функции, 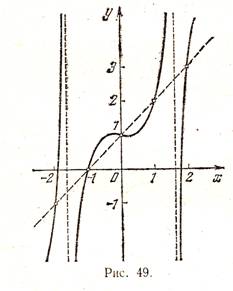 как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
как правило, поступают следующим образом. Сначала изучают свойства данной функции, с помощью которых можно построить эскиз графика. Затем, вычисляя значения функции в нескольких точках (выбор которых зависит от установленных свойств функции), находят соответствующие точки графика. И, наконец, через построенные точки проводят кривую, используя свойства данной функции.
Некоторые (наиболее простые и часто используемые) свойства функций, применяемые для нахождения эскиза графика, мы рассмотрим позже, а сейчас разберем некоторые часто применяемые способы построения графиков.
График функции у = |f(x)|.
Нередко приходится строить график функции y = |f(x) |, где f(х) -заданная функция. Напомним, как это делается. По определению абсолютной величины числа можно написать
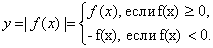
Это значит, что график функции y =|f(x)| можно получить из графика, функции y = f(x) следующим образом: все точки графика функции у = f(х), у которых ординаты неотрицательны, следует оставить без изменения; далее, вместо точек графика функции y = f(x), имеющих отрицательные координаты, следует построить соответствующие точки графика функции у = -f(x) (т. е. часть графика функции
y = f(x), которая лежит ниже оси х, следует симметрично отразить относительно оси х).
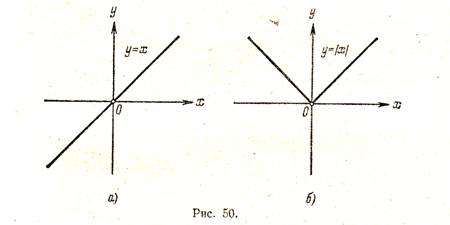
Пример 2. Построить график функции у = |х|.
Решение.
Берем график функции у = х (рис. 50, а) и часть этого графика при х < 0 (лежащую под осью х) симметрично отражаем относительно оси х. В результате мы и получаем график функции у = |х| (рис. 50, б).
Пример 3. Построить график функции y = |x2 - 2x|.
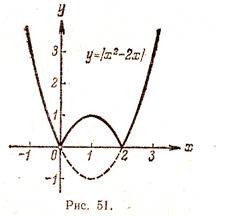 Сначала построим график функции y = x2 - 2x. График этой функции - парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х2—2х|, исходя из графика функции у = х2 — 2x
Сначала построим график функции y = x2 - 2x. График этой функции - парабола, ветви которой направлены вверх, вершина параболы имеет координаты (1; -1), ее график пересекает ось абсцисс в точках 0 и 2. На промежутке (0; 2) фукция принимает отрицательные значения, поэтому именно эту часть графика симметрично отразим относительно оси абсцисс. На рисунке 51 построен график функции у = |х2—2х|, исходя из графика функции у = х2 — 2x
Обратная функция
Если поменять ролями аргумент и функцию, то x станет функцией от y. В этом случае говорят о новой функции, называемой обратной функцией. Предположим, мы имеем функцию:
v = u 2,
где u - аргумент, a v - функция. Если поменять их ролями, то мы получим u как функцию v:
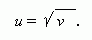
Если обозначить аргумент в обеих функциях через x, а функцию – через y, то мы имеем две функции:
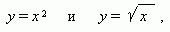
каждая из которых является обратной по отношению к другой.
П р и м е р ы. Эти функции являются обратными друг к другу:
1) sin x и Arcsin x, так как, если y = sin x, то x = Arcsin y;
2) cos x и Arccos x, так как, если y = cos x, то x = Arccos y;
3) tan x и Arctan x, так как, если y = tan x, то x = Arctan y;
4) ex и ln x, так как, если y = ex, то x = ln y.
Сложная функция
Рассмотрим функцию:
y = sin 2 (2 x).
Фактически эта запись означает следующую цепочку функциональных преобразований:
u = 2 x --> v = sin u --> y = v 2,
что может быть записано в общем виде с помощью символов функциональных зависимостей:
u = f 1(x) --> v = f 2 (u) --> y = f 3(v),
или короче:
y = f { v [ u (x) ] }.
Мы имеем здесь не одно правило соответствия для преобразования x в y, а три последовательных правила соответствия (т.е. функции), используя которые мы получаем y как функцию от x. В этом случае мы говорим, что y – сложная функция от x.
Элементарные функции
Из основных функции новые функции могут быть получены двумя способами при помощи: а) алгебраических действий; б) операции образования сложной функции.
Определение. Функции, построенные из основных элементарных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными.
1) 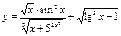 - элементарная функция, т.к число операций сложения, вычитания0 умножения, деления и образования сложной функции
- элементарная функция, т.к число операций сложения, вычитания0 умножения, деления и образования сложной функции  конечно.
конечно.
2) 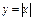 - неэлементарная функция.
- неэлементарная функция.
Основные элементарные функции
1) Постоянная функция: y = b.
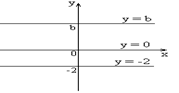
| Графиком постоянной функции y = b является прямая, параллельная оси абсцисс и проходящая через точку (0; b) на оси ординат. |
2) Степенная функция.
а) Степенная функция с натуральным показателем 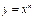 (n – натуральное число:
(n – натуральное число: 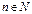 ). (непериодическая)
). (непериодическая)
n – четное число
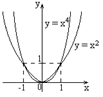 Область определения
Область определения 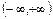 .
Область значений .
Область значений 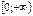 .
Монотонность: убывает на .
Монотонность: убывает на 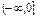 , возрастает на , возрастает на 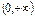 .
Четная. .
Четная.
| n – нечетное число
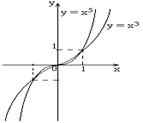 Область определения
Область определения 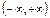 .
Область значений .
Область значений 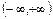 .
Монотонность: возрастает на .
Монотонность: возрастает на 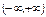 .
Нечетная. .
Нечетная.
|
б) Степенная функция с целым отрицательным показателем 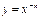 (n – натуральное число:
(n – натуральное число: 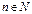 ). (непериодическая)
). (непериодическая)
n – четное число
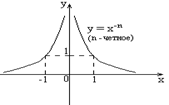 Область определения
Область определения 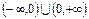 .
Область значений .
Область значений 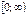 .
Монотонность: возрастает на .
Монотонность: возрастает на 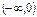 , убывает на , убывает на 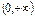 .
Четная. .
Четная.
| n – нечетное число
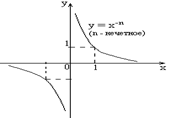 Область определения
Область определения 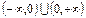 .
Область значений .
Область значений 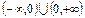 .
Монотонность: убывает на .
Монотонность: убывает на 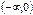 и на и на 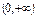 .
Нечетная. .
Нечетная.
|
в) Степенная функция с положительным показателем меньше единицы 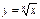 (n – натуральное число больше единицы:
(n – натуральное число больше единицы: 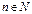 ;
; 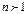 ). (непериодическая).
). (непериодическая).
n – четное число
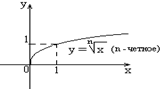 Область определения
Область определения 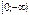 .
Область значений .
Область значений 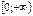 .
Монотонность: возрастает на .
Монотонность: возрастает на 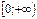 .
Общего вида. .
Общего вида.
| n – нечетное число
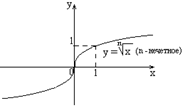 Область определения
Область определения 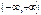 .
Область значений .
Область значений 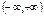 .
Монотонность: возрастает на .
Монотонность: возрастает на 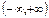 .
Нечетная. .
Нечетная.
|
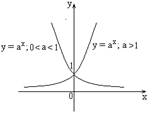
3) Показательная функция 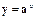
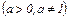 .(непериодическая).
.(непериодическая).
|
Область определения 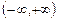 .
Область значений .
Область значений 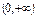 .
Монотонность: возрастает на .
Монотонность: возрастает на 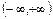 , если , если 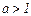 ; убывает на ; убывает на 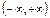 , если , если 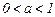 .
Общего вида. .
Общего вида.
|
4) Логарифмическая функция 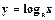
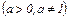 .(непериодическая).
.(непериодическая).
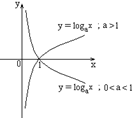
| Область определения 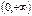 .
Область значений .
Область значений 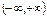 .
Монотонность: возрастает на .
Монотонность: возрастает на 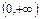 , если , если 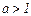 ; убывает на ; убывает на 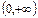 , если , если 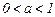 .
Общего вида. .
Общего вида.
|
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 1216; Нарушение авторских прав?; Мы поможем в написании вашей работы!