Гипербола

Эллипс

Окружность

Определение

Кривые второго порядка

Кривой второго порядка называется линия, определяемая уравнением второй степени относительно текущих декартовых координат.
В общем случае это уравнение имеет следующий вид:

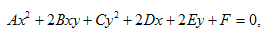
при этом предполагается, что хотя бы один из коэффициентов А, B, C не равен нулю.

Любая линия второго порядка представляет либо окружность, либо эллипс, либо гиперболу, либо параболу. Другие случаи линий второго порядка называются вырожденными.

Простейшей кривой является окружность. Ее уравнение имеет вид:

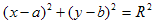
Это уравнение второй степени относительно х и у. Следовательно, окружность есть кривая второго порядка.

Определение.
Эллипсом называется множество точек плоскости, сумма расстояний от которых до двух данных точек плоскости, называемых фокусами, есть величина постоянная.

Обозначим фокусы через F₁ и F₂, расстояние между ними 2c, а постоянную величину, равную сумме расстояний от каждой точки эллипса до фокуса, через 2a (по условию 2a >2c).

Построим декартову систему координат так, чтобы фокусы F₁ и F₂ оказались на оси абсцисс, а начало координат совпало с серединой отрезка F₁F₂. В выбранной таким образом системе координат фокусы имеют координаты: левый фокус F₁(-c, 0) и правый F₂ (c,0).

Пусть М(х,у) – произвольная точка эллипса. По определению сумма расстояний от этой точки до фокусов равна 2a. Исходя из этого определения и введя обозначение: a²- c²= b², получим уравнение эллипса:

Оно называется каноническим уравнением эллипса.

Определение. Гиперболой называется множество всех точек плоскости, абсолютная величина разности расстояний каждой из которых от двух данных точек этой плоскости, называемых фокусами, есть величина постоянная.

Расстояние между фокусами F₁ и F₂ обозначим 2с, а постоянную величину, равную модулю разности расстояний от каждой точки гиперболы до фокусов 2а (0<2a <2c). Как и в случае эллипса, ось абсцисс проведем через фокусы, а за начало координат примем середину отрезка F₁F₂. Фокусы в этой системе координат имеют координаты F₁(- c, 0) и F₂(c, 0). Основываясь на определение эллипса и вводя обозначение c²-a²=b², получим уравнение гиперболы:

Уравнение называется каноническим уравнением гиперболы.

Прямые 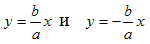называются асимптотами гиперболы.

Отношение длины фокальной оси к длине действительной оси
называется эксцентриситетом гиперболы и обозначается

Дата добавления: 2015-04-24