
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Двумя проекциями
|
|
|
|
Двумя плоскостями (a; b).
Прямая на плоскости, способы задания
| Способы графического задания прямой линии | 
|
Для определения положения прямой в пространстве существуют следующие методы:
1.Двумя точками (А и В).
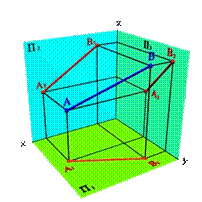
Рассмотрим две точки в пространстве А и В (рис. 15). Через эти точки можно провести прямую линию. Для того чтобы найти проекции отрезка [BA] на плоскости проекций необходимо найти проекции точек А и В и соединить их прямой. Каждая из проекций отрезка на плоскости проекций меньше самого отрезка:
[A1B1]<[BA]; [A2B2]<[BA;] [A3B3]<[BA].
 а) модель а) модель
| б) эпюр 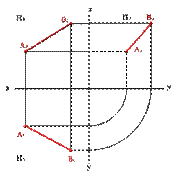
|
| Рисунок 15.Определение положения прямой по двум точкам |
Обозначим углы между прямой и плоскостями проекций через α - с плоскостью П1, β - с плоскостью П2, γ- с плоскостью П3 и тогда получим:
|А1В1|=|BA|cos a
|A2B2|=|AB|cos b
|A3B3|=|AB|cos g.
Частный случай |A1B1|=|A2B2|=|A3B3| при таком соотношении прямая образует с плоскостями проекций равные между собой углы a=b=g=350, при этом каждая из проекций расположена под углом 450 к соответствующим осям проекций.
Этот способ задания определяется тем что две непараллельные плоскости пересекаются в пространстве по прямой линии (этот способ подробно рассматривается в курсе элементарной геометрии).
Пусть в плоскостях П1 и П2 даны проекции прямых заданных отрезками [А1В1] и [A2B2]. П роведем через эти прямые плоскости a и b перпендикулярные плоскостям проекций. В том случае если эти плоскости непараллельные (рис.16а), линией их пересечения будет прямая заданная отрезком [АВ], проекциями которой являются отрезки [А1В1] и [А2В2].

| 
| |
| а)a яаньлелларапен b | б) a и b тюадапвос | |
| Рисунок 16.Определение положения прямой в пространстве по двум проекциям отрезка |
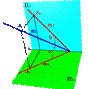
| Плоскости a и b могут слиться в одну плоскость g, если, например, проекции [ А 1 В 1] и [ А 2 В 2] перпендикулярны оси x и пересекают ее в одной точке (рис.16б). Прямая линия в этом случае будет однозначно определена своими проекциями, если на каждой из них обозначить две какие-либо точки. Если же обозначений не делать, то за искомую прямую можно принять любую прямую, лежащую в этой плоскости при условии, что она непараллельная ни одной из плоскостей проекций. Точка К, в данном случае - точка пересечения прямой с плоскостью П 2. 4. Точкой и углами наклона к плоскостям проекций. Зная координаты точки принадлежащей прямой и углы наклона ее к плоскостям проекций можно найти положение прямой в пространстве(рис.17). | |||
| Рисунок 17. Определение положения прямой по точке и углам наклона к плоскостям проекций | ||||
| положение прямой линии относительно плоскостей проекций | 
| |||
Прямая по отношению к плоскостям проекций она может занимать как общее, так и частные положения.
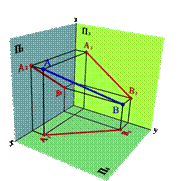
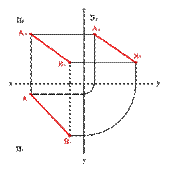
1. Прямая не параллельная ни одной плоскости проекций называется прямой общего положения (рис.18).
| 
| ||
| а) модель | б) эпюр | ||
| Рисунок 18. Прямая общего положения |
2. Прямые параллельные плоскостям проекций, занимают частное положение в пространстве и называются прямыми уровня. В зависимости от того, какой плоскости проекций параллельна заданная прямая, различают:
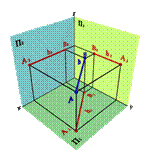
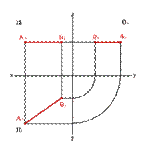
2.1. Прямые параллельные горизонтальной плоскости проекций называются горизонтальными или горизонталями (рис.19). Для любой пары точек горизонтали должно быть справедливо равенство
zA=zB Þ A2B2//0x; A3B3//0y Þ xAx–B≠, yAy–B≠, zAz–B.=
| 
| 
| ||
| а) модель | б) эпюр | |||
| Рисунок 19. Горизонтальная прямая | ||||
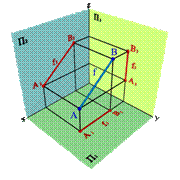
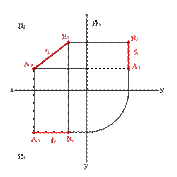
2.2. Прямые параллельные фронтальной плоскости проекций называются фронтальными или фронталями (рис.20).
yA=yBÞ A 1 B 1,x A 3 B 3z Þ xAx–B≠, yAy–B,= zAz–B≠.
| 
| 
| ||
| а) модель | б) эпюр | |||
| Рисунок 20. Фронтальная прямая | ||||
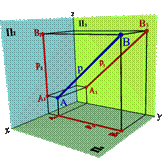
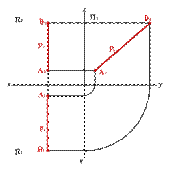
2.3. Прямые параллельные профильной плоскости проекций называются профильными (рис. 21).
xA=xB Þ A 1 B 1,y A 2 B 2z Þ xAx–B,= yAy–B≠, zAz–B≠.
Различают восходящую и нисходящую профильные прямые. Первая по мере удаления от зрителя поднимается, вторая - понижается.
| 
| 
| ||
| а) модель | б) эпюр | |||
| Рисунок 21. Профильная прямая | ||||
3. Прямые перпендикулярные плоскостям проекций, занимают частное положение в пространстве и называются проецирующими. Прямая перпендикулярная одной плоскости проекций, параллельна двум другим. В зависимости от того, какой плоскости проекций перпендикулярна исследуемая прямая, различают:
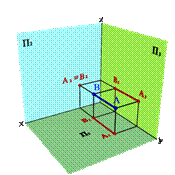
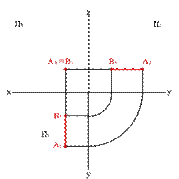
3.1. Фронтально проецирующая прямая - АВ. сир(22)
xAx–B=ü
yAy–B≠ý
zAz–B=þ,
| 
| 
| ||
| а) модель | б) эпюр | |||
| Рисунок 22. Фронтально проецирующая прямая | ||||
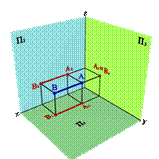
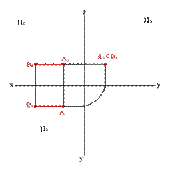
3.2. Профильно проецирующая прямая - АВ (рис.23)
xАx–B≠ü
yАy–B=ý
zАz–B=þ,
| 
| 
| ||
| а) модель | б) эпюр | |||
| Рисунок 23. Профильно-проецирующая прямая | ||||
3.3. Горизонтально проецирующая прямая - АВ (рис.24)
xАx–В=ü
yАy–В=ý
zАz–В≠þ.
| А | 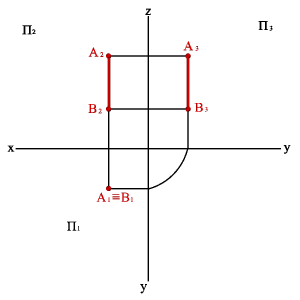
| 
| |
| а) модель | б) эпюр | ||
| Рисунок 24. Горизонтально-проецирующая прямая |
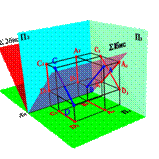
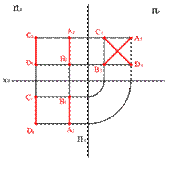
4. Прямые параллельные биссекторным плоскостям (рис. 25)
АВ S1бис Þ xAx–B=; zBz–Ay=By–A;
СD S2бис Þ xСx–D=; zD–zC=yC–yD.
Биссекторной плоскостью называется плоскость, проходящая через ось 0х и делящая двухгранный угол между плоскостями проекций П1 и П2 пополам. Биссекторная плоскость проходящая через 1 и 3 четверти называется первой биссекторной плоскостью (S1бис), а через 2 и 4 четверти - второй (S2бис).
5. Прямые перпендикулярные биссекторным плоскостям (рис. 25)
АВ S^2бис Þ xAx–B=; zBz–Ay=Вy–А;
СD S^1бис Þ xСx–D=; zDz–Cy=Cy–D.
| 
| 
| ||||
| а) модель | б) эпюр | |||||
| Рисунок 25. Прямые параллельные и перпендикулярные биссекторным плоскостям | ||||||
| следы прямой линии | ||||||
Следом прямой линии называется точка (рис. 26), в которой прямая пересекается с плоскостью проекций (так как след - точка, принадлежащая одной из плоскостей проекций, то одна из её координат должна быть равна нулю).
Горизонтальный след - М (zM)=- точка пересечения прямой с горизонтальной плоскостью проекций.
Фронтальный след - N y(N)= - точка пересечения прямой с фронтальной плоскостью проекций.
Профильный след - Т (xТ)= - точка пересечения прямой с профильной плоскостью проекций.
 а) модель а) модель
| б) 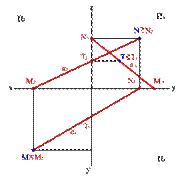 эпюр эпюр
|
| Рисунок 26.Следы прямой линии в системе трех плоскостей проекций |
Следы прямой являются точками частного положения. Одноименные проекции следа прямой совпадают с самим следом, а другие проекции лежат на осях. Например, фронтальный след прямой N2ºN, а N1 лежит на оси x, N3 - на оси z. Отмеченные особенности в расположении следов проекций позволяет сформулировать следующие правила:
|
|
|
|
|
Дата добавления: 2015-04-24; Просмотров: 604; Нарушение авторских прав?; Мы поможем в написании вашей работы!