Если прямые не пересекаются и не параллельны между собой, то точка пересечения их одноименных проекций не лежит на одной линии связи

Для построения фронтального следа N прямой нужно из точки пересечения горизонтальной проекции её с осью 0x восстановить перпендикуляр до пересечения с фронтальной проекцией прямой.

Для построения горизонтального следа М прямой необходимо продолжить ее фронтальную проекцию до пересечения с осью x и в этой точке восстановить перпендикуляр к оси до пересечения с горизонтальной проекцией прямой.

			С помощью этих правил найдены на эпюре следы прямой а(рис.27). Здесь же показаны совпавшие проекции точки А, принадлежащей рассматриваемой прямой. Особенность этой точки в том, что она равноудалена от плоскостей проекций, то есть находятся в биссекторной плоскости S2бис. Следы прямой, являются точками, в которых прямая переходит из одного октанта в другой, позволяют отмечать её видимость. Видимой частью прямой будет та, которая расположена в пределах первого октанта.
	Рисунок 27. Нахождение горизонтального и фронтального следов прямой линии
Взаимное расположение точки и прямой

Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой). Из четырех предложенных на рисунке 28 точек, только одна точка С лежит на прямой АВ.

а) эпюр	б) модель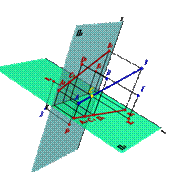
Рисунок 28. Взаимное расположение точки и прямой

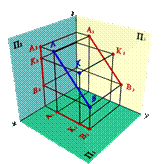
В тех случаях, когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П ₁, П ₂ и П ₃), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П ₁, П ₂ или П ₃. Например, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости проекций (рис.29).

а) эпюр	б) модель
Рисунок 29. Точка и прямая, расположенные в профильной плоскости уровня

Из свойств параллельного проецирования известно, что если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же соотношении.

Зная это условие можно определить принадлежность точки К прямой АВ:

А ₂ К ₂ / К ₂ В ₂ ¹ А ₁ К ₁/ К ₁ В ₁ Þ К Ï АВ

Взаимное расположение двух прямых

Прямые линии в пространстве могут быть параллельными, пересекающимися и скрещивающимися. Рассмотрим подробнее каждый случай.

1. Параллельные прямые линии.

Параллельными называются две прямые, которые лежат в одной плоскости и не имеют общих точек.

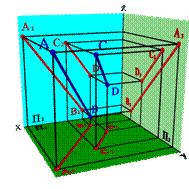
Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если ABCD то A₁B₁C₁D₁; A₂B₂C₂D₂; A₃B₃C₃D₃ (рис.33). В общем случае справедливо и обратное утверждение.

а) модель	б) эпюр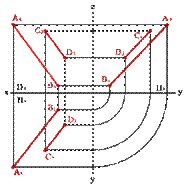
Рисунок 33. Параллельные прямые

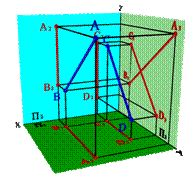
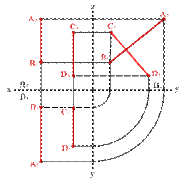
Особый случай представляют собой прямые, параллельные одной из плоскостей проекций. Например, фронтальные и горизонтальные проекции профильных прямых параллельны, но для оценки их взаимного положения необходимо сделать проекцию на профильную плоскость проекций (рис. 34). В рассмотренном случае проекции отрезков на плоскость П₃ пересекаются, следовательно, они не параллельны.

Решение этого вопроса можно получить сравнением двух соотношений если:

А₂В₂/ А₁В₁= С₂Д₂/ С₁ Д₁ Þ АВ//СД

А₂В₂/ А₁В₁ ¹ С₂Д₂/ С₁Д₁ Þ АВ # СД

а) модель	б) эпюр
Рисунок 34. Прямые параллельные профильной плоскости проекций

2. Пересекающиеся прямые.

Пересекающимися называются две прямые лежащие в одной плоскости и имеющие одну общую точку.

Если прямые пересекаются, то точки пересечения их одноименных проекций находится на одной линии связи (рис. 35).

а) модель	б) эпюр
Рисунок 35. Пересекающиеся прямые

В общем случае справедливо и обратное утверждение, но есть два частных случая:

1. Если одна из прямых параллельна какой-либо из плоскостей проекций, например, профильной (рис.36), то по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, однако сами отрезки не пересекаются, потому что точка пересечения профильных проекций этих отрезков не лежит на одной линии связи с точками пересечения их горизонтальной и фронтальной проекций.

а) модель	б) эпюр
Рисунок 36. Одна из прямых параллельна профильной плоскости проекций

2. Пересекающие прямые расположены в общей для них проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций (рис. 37).

О взаимном расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции (А ₁ В ₁∩ С ₁ D ₁Þ АВ∩СD).

а) модель	б) эпюр
Рисунок 37. Пересекающиеся прямые расположены в фронтально проецирующей плоскости

3. Скрещивающиеся прямые

Скрещивающимися называются две прямые не лежащие в одной плоскости.

Точке пересечения фронтальных проекций прямых (рис. 38) соответствуют две точки А и В, из которых одна принадлежит прямой а, другая в. Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки А и В находятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точка В, лежащая на прямой в, следовательно, прямая в проходит в этом месте ближе прямой а и фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и D решение аналогично).

Этот способ определения видимости по конкурирующим точкам. В данном случае точки А и В - фронтально конкурирующие, а С и D - горизонтально конкурирующие.

а) модель	б) эпюр
Рисунок 38. Скрещивающиеся прямые

13. Расположение прямой на плоскости

1) Прямая проходит через начало координат О (0;0) Ах+Вх=0

2) Прямая параллельна оси (ох): Ву + С=0

3) Прямая параллельна оси (оу): Ах+ С=0

Взаимное расположение 2-х прямых А₁х+В₁у+С₁=0 и А₂х+В₂у+С₂=0

1) Прямые совпадают: А₁ / А₂=В₁ / В₂=С₁ / С₂

2) Прямые параллельны: А1 / А2=В1 / В2≠С1 / С2

3) Прямые пересекаются: если нет пропорций коэффициентов у = К₁х+в₁ и у=К₂х+в₂

- прямые совпадают: К₁=К₂ и в₁=в₂
- прямые параллельны: К₁=К₂

- прямые перпендикулярны: К₁К₂= -1

Основные задачи прямой на плоскости

1) Точка пересечения 2-х прямых: { А₁х+В₁у+С₁=0

А₂х+В₂у+С₂=0

- если единственное решение (х_о, у_о)- это точка пересечения

- если нет решений, то прямые параллельны

- если бесконечное множество решений, то прямые совпадают

2) Расстояние от точки М_о (х_о, у_о)до прямой Ах+Ву+С=0 d=│Ах_о+Ву_о+С│ / корень из А²+В²

Расстояние между параллельными прямыми: берём производную точку1-ой прямой и находим расстояние от неё до другой

3) Угол между прямыми v

а) А₁х+В₁у+С₁=0 и А₂х+В₂х+С₂=0

Cos v=А₁ × А₂+В₁×В₂ / корень изА₁²+В₁² × на корень из А₂²+В₂² – угол между параллельными векторными прямыми.

б) у=К₁х+в₁ и у=К₂х+в₂

tg v= К₂-К₁ / 1 - К₁К₂

4) Геометрический смысл знаков трёхчленаАх+Ву+С, (взаимное расположение точки и прямой).точка Мо(х_о,у_о) и прямая А_х+В_у+С=0

- если Ах_о+Ву_о+С>0, то М_о выше прямой

- если Ах_о+Ву_о+C<0, то точка М_о ниже прямой

- если Ах_о+Вх_о +С=0, то точка М_о лежит на прямой

Дата добавления: 2015-04-24