Основные задачи в пространстве: углы, условие параллельности и перпендикулярности

Способы задания прямой в пространстве

Способы задания и расположение плоскости в пространстве

Парабола.

Параболой называется множество всех точек плоскости, равноудаленных от данной точки F, называемой фокусом, и данной прямой, называемой директрисой.

Обозначим расстояние от фокуса до директрисы р. Эта величина называется параметром параболы. Фокус имеет координаты (р/2,0), а уравнение директрисы имеет вид x=p/2.

Тогда уравнение параболы запишется в виде:

y²=2px

Данное уравнение называется каноническим уравнением параболы.

Способы задания плоскостей

Рассмотрим некоторые способы графического задания плоскости. Положение плоскости в пространстве может быть определено:

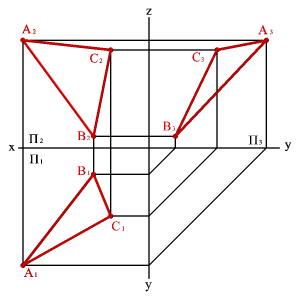
1. тремя точками, не лежащими на одной прямой линии (рис.41);

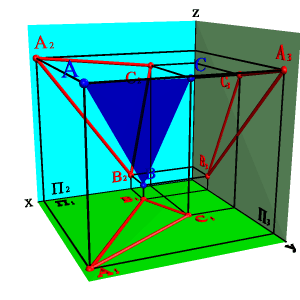
а) модель	б) эпюр
Рисунок 41. Плоскость, заданная тремя точками, не лежащими на одной прямой

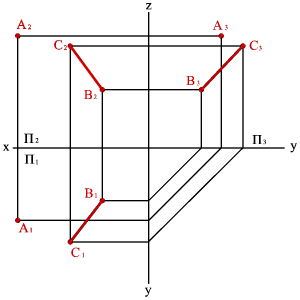
2. прямой линией и точкой, не принадлежащей этой прямой (рис.42);

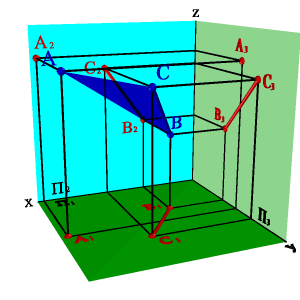
а) модель	б) эпюр
Рисунок 42. Плоскость, заданная прямой линией и точкой, не принадлежащей этой линии

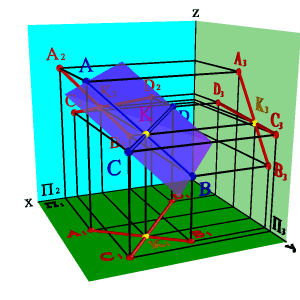
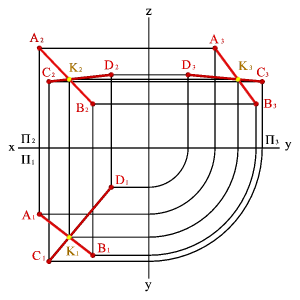
3. двумя пересекающимися прямыми (рис.43);

а) модель	б) эпюр
Рисунок 43. Плоскость, заданная двумя пересекающимися прямыми

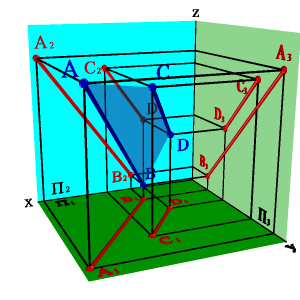
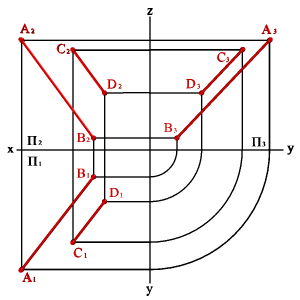
4. двумя параллельными прямыми (рис.44);

а) модель	б) эпюр
Рисунок 44. Плоскость, заданная двумя параллельными прямыми

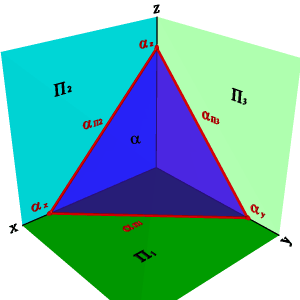
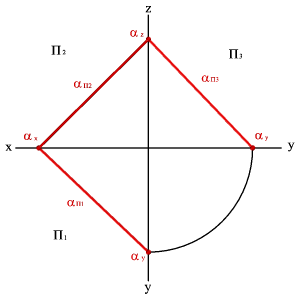
5. О положении плоскости относительно плоскостей проекций удобно судить по её следам (рис.45).

Следом плоскости называется прямая линия, по которой плоскость пересекается с плоскостью проекций. В зависимости от того, какую плоскость проекций пересекает данная a плоскость различают горизонтальный a _П1, фронтальный a _П2 и профильный a _П3 следы.

а) модель	б) эпюр
Рисунок 45. Плоскость, заданная следами

Следы плоскости общего положения пересекаются попарно на осях в точках a_x,a_y,a_z. Эти точки называются точками схода следов, их можно рассматривать как вершины трехгранных углов, образованных данной плоскостью с двумя из трех плоскостей проекций.

Каждый из следов плоскости совпадает со своей одноименной проекцией, а две другие разноименные проекции лежат на осях.

положение плоскости относительно плоскостей проекций

В зависимости от положения плоскости по отношению к плоскостям проекций она может занимать как общее, так и частные положения.

1. Плоскость не перпендикулярная ни одной плоскости проекций называется плоскостью общего положения. Такая плоскость пересекает все плоскости проекций (имеет три следа: - горизонтальныйa_П1; - фронтальный a_П2; - профильный a_П3).

2. Плоскости, перпендикулярные плоскостям проекций – занимают частное положение в пространстве и называются проецирующими. В зависимости от того, какой плоскости проекций перпендикулярна заданная плоскость, различают:

2.1. Плоскость, перпендикулярная горизонтальной плоскости проекций (a ^П₁), называется горизонтально проецирующей плоскостью. Горизонтальная проекция такой плоскости представляет собой прямую линию, которая одновременно является её горизонтальным следом. Горизонтальные проекции всех точек этой плоскости совпадают с горизонтальным следом (рис.46).

а) модель	б) эпюр
Рисунок 46. Горизонтально проецирующая плоскость

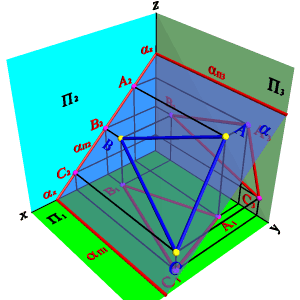
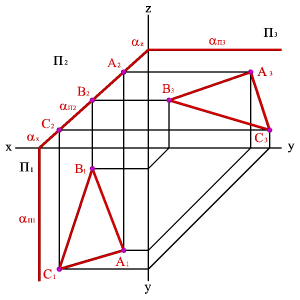
2.2. Плоскость, перпендикулярная фронтальной плоскости проекций (a^П ₂)- фронтально проецирующая плоскость. Фронтальной проекцией плоскости a является прямая линия, совпадающая со следом a_П2 (рис.47).

а) модель	б) эпюр
Рисунок 47. Фронтально проецирующая плоскость

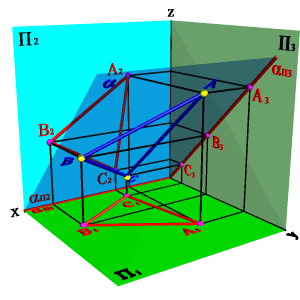
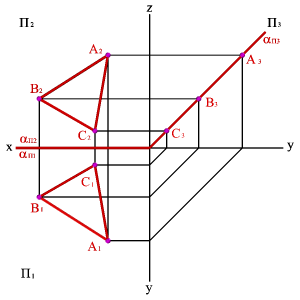
2.3. Плоскость, перпендикулярная профильной плоскости (a^П ₃) - профильно проецирующая плоскость. Частным случаем такой плоскости является биссекторная плоскость (рис.48).

а) модель	б) эпюр
Рисунок 48. Биссекторная плоскость

3. Плоскости, параллельные плоскостям проекций – занимают частное положение в пространстве и называются плоскостями уровня. В зависимости от того, какой плоскости параллельна исследуемая плоскость, различают:

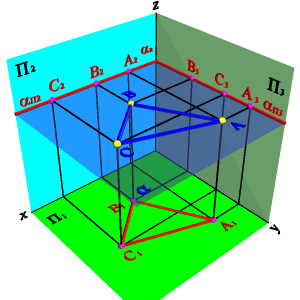
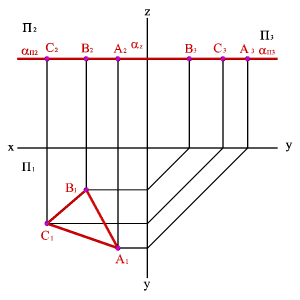
3.1. Горизонтальная плоскость - плоскость, параллельная горизонтальной плоскости проекций (aП ₁) - (a^П₂,a^П₃). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П ₁ без искажения, а на плоскости П₂ и П₃ в прямые - следы плоскости a_П2 и a_П3 (рис.49).

а) модель	б) эпюр
Рисунок 49. Горизонтальная плоскость

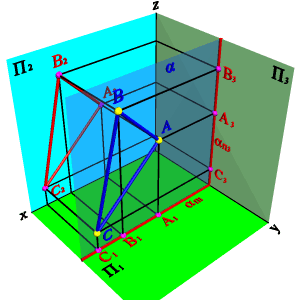
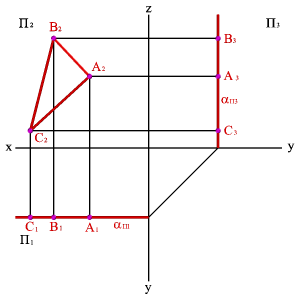
3.2. Фронтальная плоскость - плоскость, параллельная фронтальной плоскости проекций (aП₂), (a^П₁, a^П₃). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П ₂ без искажения, а на плоскости П ₁ и П ₃ в прямые - следы плоскости a_П1 и a_П3 (рис.50).

а) модель	б) эпюр
Рисунок 50. Фронтальная плоскость

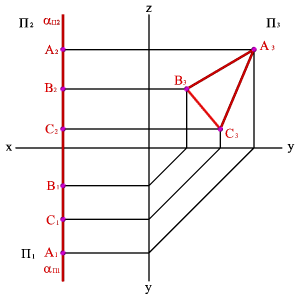
3.3. Профильная плоскость - плоскость, параллельная профильной плоскости проекций (a//П₃), (a^П₁, a^П₂). Геометрический объект, принадлежащий этой плоскости проецируется на плоскость П ₃ без искажения, а на плоскости П₁ и П₂ в прямые - следы плоскости a_П1 и a_П2 (рис.51).

а) модель	б) эпюр
Рисунок 51. Профильная плоскость

Следы плоскости

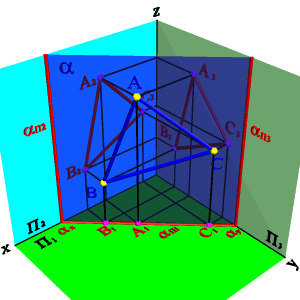
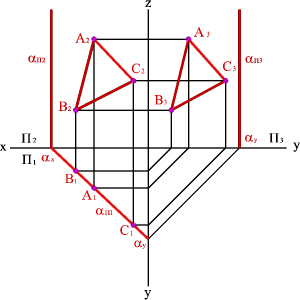
Следом плоскости называется линия пересечения плоскости с плоскостью проекций. В зависимости, от того с какой из плоскостей проекций пересекается данная плоскость, различают: горизонтальный, фронтальный и профильный следы плоскости.

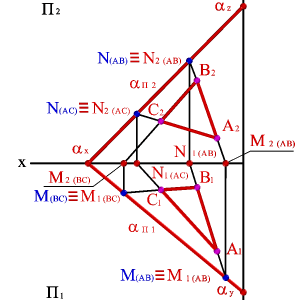
Каждыйслед плоскости является прямой линией, для построения которых необходимо знать две точки, либо одну точку и направление прямой (как для построения любой прямой). На рисунке 52показано нахождение следов плоскости α(АВС). Фронтальный след плоскости α_П2 построен, как прямая соединяющая две точки N_(АС) и N_(АВ), являющиеся фронтальными следами соответствующих прямых, принадлежащих плоскости α. Горизонтальный след α_П1 – прямая, проходящая через горизонтальные следы прямых ВС и АВ. Профильный след α_П3 – прямая соединяющая точки (α_y и α_z) пересечения горизонтального и фронтального следов с осями. Точки α_x, α_y и α_z называют точками схода следов.

а) модель	б) эпюр
Рисунок 52. Построение следов плоскости
Взаимное расположение прямой и плоскости

Известны три варианта взаимного расположения прямой и плоскости:

Прямая принадлежит плоскости.

Прямая параллельна плоскости.

Прямая пересекает плоскость.

Прямые линии, принадлежащие плоскости и занимающие частное положение по отношению к плоскостям проекций, называются главными линиями плоскости.

Очевидно, что если прямая не имеет двух общих точек с плоскостью, то она или параллельна плоскости, или пересекает ее.

Большое значение для задач начертательной геометрии имеет частный случай пересечения прямой и плоскости, когда прямая перпендикулярна плоскости.

Определение взаимного положения прямой и плоскости - позиционная задача, для решения которой применяется метод вспомогательных секущих плоскостей.

Векторно-параметрическое уравнение прямой

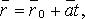
где 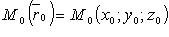- фиксированная точка, лежащая на прямой; - направляющий вектор.

В координатах (параметрические уравнения):

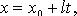
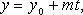
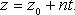
Канонические уравнения прямой

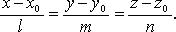
Уравнения прямой по двум точкам

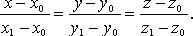
Прямая как линия пересечения двух плоскостей

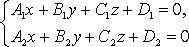
при условии, что не имеют места равенства

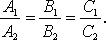
Направляющий вектор такой прямой

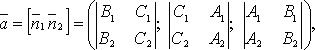
где

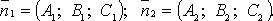
Условия параллельности двух прямых:

а) Если прямые заданы уравнениями xCOSa+ySINa–P=0 с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k1 = k2.

б) Для случая, когда прямые заданы уравнениями в общем виде A1x + B1y + C1 = 0, A2x + B2y + C2 = 0, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

=

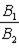
Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями xCOSa+ySINa–P=0 с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

= –

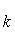Это условие может быть записано также в виде

k1k2 = -1.

б) Если уравнения прямых заданы в общем виде A1x + B1y + C1 = 0, A2x + B2y + C2 = 0, то условие их перпендикулярности (необходимое и достаточное) заключается в выполнении равенства

A1A2 + B1B2 = 0. A1A2 + B1B2 = 0.

Дата добавления: 2015-04-24