Пример. Этот метод называется иногда еще методом одновременных смещений и является самым простым из итерационных методов

Метод Якоби

Этот метод называется иногда еще методом одновременных смещений и является самым простым из итерационных методов. Однако пользуются им редко, так как он обладает медленной сходимостью. Мы рассмотрим его потому, что он позволяет лучше понять алгоритм других итерационных процессов.

Метод состоит в выполнении следующих операций:

1) От узла к узлу с помощью вычислительного шаблона производится расчет новых значений переменных по старым, пока не будут получены значения во всех узлах.

2) Затем производится одновременная замена значений переменных во всех узлах сетки. Поскольку новые значения искомого решения вводятся одновременно во всех узлах сетки, порядок, в котором производятся вычисления, не имеет значения.

3) Вычисления заканчиваются, когда изменение значений переменных во всех узлах становится меньше некоторой заранее заданной величины.

Любой итерационный метод требует задания начального приближенного решения, которое может быть получено любым разумным способом. Часто для получения приближенных значений переменных в узлах сетки пользуются линейной интерполяцией. Очевидно, чем ближе исходное приближение к решению, тем меньше итераций необходимо для его получения. Для пояснения метода одновременных смещений рассмотрим пример.

Пусть требуется найти стационарное распределение температуры квадратной пластины со стороной, равной 1.

Заданные граничные условия на краях пластины:

при x = 0.0 и любых значениях y: T = 0.0,

при y = 0.0 и любых значениях x: T = 100*x,

при x = 1.0 и любых значениях y: T = 100,

при y = 1.0 и любых значениях x: T = 100*x2

Распределение температуры в подобных случаях описывается уравнением Лапласа с двумя независимыми переменными.

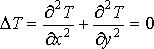
Чтобы решить задачу, введем на плоскости двумерную сетку N на N. Пусть N=5. Расстояния между соседними узлами h =1/(N-1)=0.25. Сетка содержит 25 узлов, в 16 из которых задано значение температуры согласно граничным условиям. Расположение узлов показано на рисунке. Цифрами около соответствующих узлов сетки обозначены значения температуры на границе.

Задача состоит в определении потенциала во всех внутренних узлах. (Для N=5 их 9 штук.)

Новое значение потенциала в узле можно найти с помощью крестообразного вычислительного шаблона.

Ti,j = (Ti-1,j + Ti+1,j + Ti,j-1 + Ti,j+1) / 4

Начальные значения потенциала во внутренних узлах сетки зададим нулевыми. Истинные значения T будем искать методом итераций. Конечно, N=5 очень мало, и такое число узлов приведено только для простоты схематического рисунка. Мы начнем свои расчеты с N=8.

Получив удовлетворительное решение, можно с помощью линейной интерполяции найти значения потенциала в пространстве между узлами.

Для решения этой задачи была написана программа на языке пакета Scilab

Местонахождение документации на русском языке

Текст программы

// File laplas.sce

//задача Дирихле для уравнения Лапласа delta_u=0

//--------------

//ОПИСАНИЕ ПРОГРАММЫ

// область решений -квадрат с вершинами (x0,y0), (xn,y0),(xn,y0),(xn,yn)

//n - число узлов сетки по оси x (совпадает с числом узлов по оси y)

// h-шаг сетки (h=(xn-x0)/(n-1))

// eps -задаваемая точность

// u0(i,j) -начальное приближения для решения в узле с кординатами x(i) и y(j)

// u(i,j) -решение в узле с кординатами x(i) и y(j)

// delta_max - норма L(infinity), оценивающая разницу между соседними итерациями

// Требование прекращение счета delta_max < eps (условие сходимости)

// Во избежание зацикливания задается максимально возможное значение количества итераций max_iter.

//--------------------------------

n=128;

x0=0;xn=1;

y0=0;yn=1;

h=(xn-x0)/(n-1); // шаг сетки

x=x0:h:x0+(n-1)*h; // вектор принимаемых значений x

y=y0:h:y0+(n-1)*h; // вектор принимаемых значений y

// граничные условия при x=x0 и xn=x0+n*h

u0=zeros(n,n); // начальные значения внутри сетки

u0(:,1)=0;

u0(:,n)=100;

//добавляем граничные условия при x=x0 и xn=x+n*h

//добавляем граничные условия при y=y0 и yn=y+n*h

for j=1:n

u0(1,j)=100*x(j);

u0(n,j)=100*x(j)^2;

end;

u=u0; // первое приближение

eps=0.01;

delta_max=eps+1; // это просто так, чтобы она была >eps

num_iter=0; // счетчик номера итераций

max_iter=5000; // максимально допустимое число итераций

while delta_max > eps,

if num_iter> max_iter then break, end; //end if

num_iter=num_iter+1;

u_old=u; // понадобится для дальнейшего сравнения

for i = 2:(n-1), for j = 2:n-1,

u(i,j) =(u(i-1,j)+u(i+1,j)+u(i,j-1)+u(i,j+1))/4;

end; //next j

end; //next i

// delta_max - норма, оценивающая разницу между соседними итерациями (условие сходимости)

delta_max=max(abs(u_old-u));

delta(num_iter)=delta_max; // массив

end; //end while

//запись данных в файл в формате: x y u(x,y))

fd=mopen("d:\me_dat\u.dat","w");

for i = 1:n, for j = 1:n,

mfprintf(fd,"%f %f %f\n",x(i),y(j),u(j,i));

end; //next i

end; //next j

mclose(fd); //конец записи

plot2d(1:num_iter,delta); // зависимость невязки от номера итерации

Sgrayplot(x,y,u'); // график решения уравнения

Текст программы следует записать в файл с расширением.sce и запустить из сессии scilab с помощью команды exec, или из меню главного окна scilab [File] - [Exec] или (только для версии scilab 2.7) из окна редактора scipad. В результате мы будем иметь файл с данными на диске и графики в графическом окне scilab.

Результаты расчетов:

Были проведены численные расчеты для количества узлов: 8, 16, 64 и 128 для заданной точности вычислений eps=0.01.

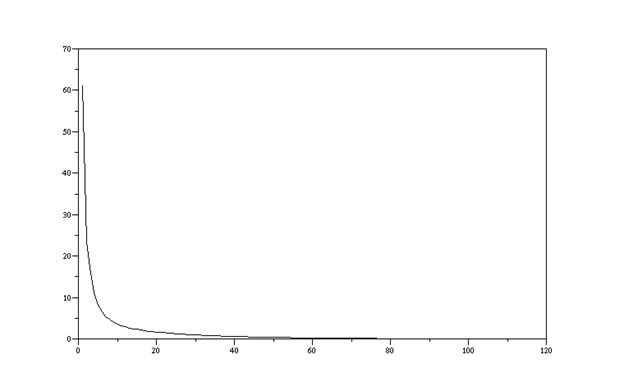
На рисунке приведена зависимость величины max(abs(u_old-u))от номера итерации, где u-матрица значений решения в узлах для текущей итерации, а u_old -для предшествующей для n=16.

В таблице приведены сравнительные характеристики необходимого числа итераций для достижения заданной точности и времени расчета в зависимости от числа узлов сетки.

Дата добавления: 2015-04-24