Метод минимальных невязок

(Одношаговый, двухшаговый - гугл не нашел L)

итерационный метод решения линейного операторного уравнения

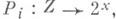
с самосопряженным положительно определенным ограниченным оператором А, действующим в гильбертовом пространстве Н, и заданным элементом 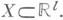. Формулы М. н. м. имеют вид

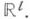где параметр 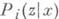выбирается на каждом шаге 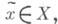из условия максимальной минимизации нормы невязки 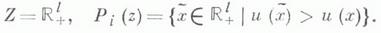т. е. требуется выполнение соотношения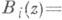

Если спектр оператора А принадлежит отрезку [ т, М] действительной оси, где 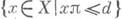- положительные числа, то последовательные приближения 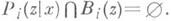метода (2) -(3) сходятся к решению 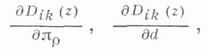уравнения (1) со скоростью геометрич. прогрессии со знаменателем

Различные способы определения в H скалярного произведения приводят к различным итерационным методам. В частности, при специальных скалярных произведениях формулы М. н. м. совпадают с формулами наискорейшего спуска метода и метода минимальных ошибок (см. [2]).

Условия сходимости М. н. м. могут быть ослаблены по сравнению с перечисленными выше: если рассматривать на нек-рых подмножествах из H.

Напр., если рассматривать М. н. м. только в действительных пространствах, то можно отказаться от требования самосопряженности оператора А(см. [3], [4]).

Дата добавления: 2015-04-24