Электрическое поле проводников

Проводник — вещество, проводящее электрический ток. Среди наиболее распространённых твёрдых проводников известны металлы, полуметаллы, углерод в виде угля и графита). Проводники бывают первого и второго рода. К проводникам первого рода относят те проводники, в которых имеется электронная проводимость (посредством движения электронов). К проводникам второго рода относят проводники с ионной проводимостью (электролиты).

Идеальный проводник – это среда с бесконечно большой удельной проводимостью (σ → ∞). Переменное электромагнитное поле не проникает в идеальный проводник, т.е. в нем E = 0 и H = 0.

Для электростатических явлений поле внутри проводника равно нулю:

E→in ≡ 0.

Механизм исчезновения электрического поля в проводниках связан со смещением свободных зарядов ровно настолько, чтобы как раз компенсировать внешнее электрическое поле, если таковое имеется. При изменении внешнего поля свободные заряды в проводнике перераспределяются, а в момент перераспределения в проводнике течет ток.

Поскольку E→in = 0, то и плотность заряда внутри проводника также равна нулю:

ρin = 1 4π divE→in ≡ 0.

Заряды, компенсирующие внешнее поле, могут размещаться только на поверхности проводника. В связи с этим говорят, что проводник квазинейтрален. По аналогии с объёмной плотностью заряда ρ = limΔV →0Δq∕ΔV, поверхностную плотность определяют, как предел отношения заряда на физически малом участке поверхности Δq к площади этого участка ΔS:

σ = limΔS→0Δq∕ΔS.

Все точки проводника имеют одинаковый потенциал, так как gradϕin = −E→in = 0. Поверхность проводника также эквипотенциальна. Следовательно, электрическое поле перпендикулярно к ней. Этот факт иногда формулируют в виде равенства нулю тангенциальной (касательной к поверхности проводника) проекции внешнего электрического поля E→t = [[n→,E→],n→].

Электростатическая защита - помещение приборов, чувствительных к электрическому полю, внутрь замкнутой проводящей оболочки для экранирования от внешнего электрического поля. Это явление связано с тем, что на поверхности проводника (заряженного или незаряженного), помещённого во внешнее электрическое поле, заряды перераспределяются так (явление электрической индукции), что создаваемое ими внутри проводника поле полностью компенсирует внешнее.

Метод изображений это способ решения основной задачи электростатики, основанный на подмене исходной конфигурации проводников некоторым другим распределением зарядов, потенциал которого на поверхности проводников и в бесконечности совпадает с граничными условиями исходной задачи. Новая задача, разумеется, должна иметь простое решение. Поскольку решение при данных граничных условиях единственно, то оно является и решением исходной задачи.

Электрическая ёмкость — характеристика проводника, характеризующая его способность накапливать электрический заряд. Ёмкость определяется как отношение величины заряда проводника к потенциалу проводника. Ёмкость обозначается как C.

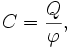
где Q — заряд, 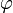— потенциал.

В системе СИ ёмкость измеряется в фарадах. В системе СГС в сантиметрах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удаленной точки принят равным нулю. Она определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость в вакууме проводящего шара радиуса R равна (в системе СИ):

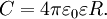
Понятие ёмкости также относится к системе проводников, в частности, к системе двух проводников, разделённых диэлектриком — конденсатору. В этом случае взаимная ёмкость этих проводников (обкладок конденсатора) будет равна отношению заряда, накопленного конденсатором, к разности потенциалов между обкладками. Для плоского конденсатора ёмкость равна:

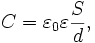
где S — площадь обкладок, d — расстояние между обкладками, ε — диэлектрическая проницаемость среды между обкладками, ε0 = 8.854*10-12 Ф/м — электрическая постоянная.

Потенциальную энергию взаимодействия двух точечных зарядов q1 и q2, находящихся в вакууме на расстоянии r12 друг от друга можно вычислить по:

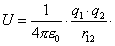
Рассмотрим систему, состоящую из N точечных зарядов: q1, q2,..., qn.

Энергия взаимодействия такой системы равна сумме энергий взаимодействия зарядов взятых попарно:

.

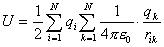В формуле суммирование производится по индексам i и k (i№k). Оба индекса пробегают, независимо друг от друга, значения от 0 до N. Слагаемые, для которых значение индекса i совпадает со значением индекса k не учитываются. Коэффициент 1/2 поставлен потому, что при суммировании потенциальная энергия каждой пары зарядов учитывается дважды. Формулу данную можно представить в виде:

,

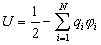где ji - потенциал в точке нахождения i-го заряда, создаваемый всеми остальными зарядами:

.

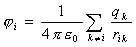Энергия взаимодействия системы точечных зарядов, вычисляемая по формуле, может быть как положительной, так и отрицательной. Например она отрицательная для двух точечных зарядов противоположного знака.

Формула определяет не полную электростатическую энергию системы точечных зарядов, а только их взаимную потенциальную энергию. Каждый заряд qi, взятый в отдельности обладает электрической энергией. Она называется собственной энергией заряда и представляет собой энергию взаимного отталкивания бесконечно малых частей, на которые его можно мысленно разбить. Эта энергия не учитывается в формуле. Учитывается только работа затрачиваемая на сближение зарядов qi, но не на их образование.

Полная электростатическая энергия системы точечных зарядов учитывает также работу, на образование зарядов qiиз бесконечно малых порций электричества, переносимых из бесконечности. Полная электростатическая энергия системы зарядов всегда положительная. Это легко показать на примере заряженного проводника. Рассматривая заряженный проводник как систему точечных зарядов и учитывая одинаковое значение потенциала в любой точке проводника, из формулыполучим:

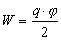. (4)

Эта формула дает полную энергию заряженного проводника, которая всегда положительна (при q>0, j>0, следовательно W>0, если q<0, то j<0, но W>0).

Предположим, что имеется непрерывное распределение зарядов, задаваемое объемной плотностью ρ(r→). Тогда в элементарном объеме dV содержится заряд

dq = ρ(r→)dV,

а формула приобретает такой вид

W = 1 2 ∫ ρ(r→)ϕ(r→)dV.

Некоторое замечание надо сделать для обоснования перехода. При переходе к объемному распределению под интегралом, вообще говоря, следовало писать

ρ(r→)ϕ′(r→),

понимая под ϕ′(r→) потенциал всех зарядов, за исключением элементарного заряда ρdV. Мысленно представим заряд ρdV в виде равномерно заряженного шарика малого радиуса δ с центром в точке r→ и с плотностью заряда ρ(r→). Легко вычислить, что потенциал этого заряда в центре шарика = 3 2 q δ = 3 2 1 δ ⋅4 3πδ3ρ = 2πδ2 ⋅ ρ(r→), и следовательно,

ϕ′(r→) = ϕ(r→) − 2πρ(r→)δ2.

Отсюда видно, что при δ → 0 ϕ′→ ϕ(r→) и замена ϕ′(r→) на ϕ(r→), таким образом, действительно допустима.

Поляризация диэлектриков — явление, связанное с ограниченным смещением связанных зарядов в диэлектрике или поворотом электрических диполей, обычно под воздействием внешнего электрического поля, иногда под действием других внешних сил или спонтанно.

Поляризацию диэлектриков характеризует вектор электрической поляризации. Физический смысл вектора электрической поляризации — это дипольный момент, отнесенный к единице объема диэлектрика. Иногда вектор поляризации коротко называют просто поляризацией.

• Вектор поляризации применим для описания макроскопического состояния поляризации не только обычных диэлектриков, но и сегнетоэлектриков, и, в принципе, любых сред, обладающих сходными свойствами. Он применим не только для описания индуцированной поляризации, но и спонтанной поляризации (у сегнетоэлектриков).

Поляризация — состояние диэлектрика, которое характеризуется наличием электрического дипольного момента у любого (или почти любого) элемента его объема.

Различают поляризацию, наведенную в диэлектрике под действием внешнего электрического поля, и спонтанную (самопроизвольную) поляризацию, которая возникает в сегнетоэлектриках в отсутствие внешнего поля. В некоторых случаях поляризация диэлектрика (сегнетоэлектрика) происходит под действием механических напряжений, сил трения или вследствие изменения температуры.

Поляризация не изменяет суммарного заряда в любом макроскопическом объеме внутри однородного диэлектрика. Однако она сопровождается появлением на его поверхности связанных электрических зарядов с некоторой поверхностной плотностью σ. Эти связанные заряды создают в диэлектрике дополнительное макроскопическое поле с напряженностью Е₁, направленное против внешнего поля с напряженностью Е₀. Результирующая напряженность поля Е внутри диэлектрика Е=Е₀-Е₁.

Дата добавления: 2015-04-24