Показатели качества информации

Возможность и эффективность использования информации обусловливаются её основными потребительскими показателями качества.

l Репрезентативность информации связана с правильностью ее отбора и формирования для отражения наиболее существенных признаков и связей изучаемого явления.

l Содержательность информации отражает её семантическую (смысловую) емкость. Характеризуется коэффициентом содержательности (C = I_c / V_д).

l Достаточность (полнота) информации означает, что она содержит минимальный, но достаточный для принятия правильного решения состав показателей.

l Доступность информации восприятию пользователя обеспечивается выполнением соответствующих процедур ее получения и преобразования. Например, в информационной системе результирующая информация преобразовывается к доступной и удобной для восприятия пользователя форме.

l Актуальность информации определяется степенью сохранения ценности информации в момент ее использования и зависит от динамики изменения ее характеристик и от интервала времени, прошедшего с момента возникновения данной информации.

l Своевременность информации означает ее поступление не позже заранее назначенного момента времени, согласованного со временем решения поставленной задачи.

l Точность информации определяется степенью близости получаемой информации к реальному состоянию объекта, процесса или явления.

l Достоверность информации определяется ее свойством отражать реально существующие объекты с необходимой точностью.

l Устойчивость информации отражает ее способность реагировать на изменения состояния объекта без нарушения необходимой точности.

11. Позиционные системы счисления: основные понятия, представление целых неотрицательных и дробных чисел.

Совокупность приемов и правил представления чисел с помощью цифровых знаков называется системой счисления.

В зависимости от способа изображения чисел системы счисления делятся на 2 типа:

l непозиционные;

l позиционные.

В непозиционных системах счисления значение любой цифры не зависит от занимаемой ею позиции в числе. Например, римская система, в которой в числе XXX каждый разряд означает 10 единиц (L – 50, C – 100, D – 500, М – 1000). В непозиционных системах счисления не представляются дробные и отрицательные числа, действия над числами связаны с большими трудностями и не имеют правил.

В позиционных системах счисления значение любой цифры в числе зависит от ее положения (позиции) в ряду цифр, изображающих это число.

Основным понятием любой позиционной системы счисления является основание. Оно показывает:

l сколько различных цифр в системе счисления;

l во сколько раз изменяется количественное значение цифры при перемещении ее на соседнюю позицию.

В зависимости от основания различают следующие системы счисления:

l десятичную (Dec) (0, 1, 2, 3,…, 9);

l восьмеричную (Oct) (0, 1, 2,…, 7);

l двоичную (Bin) (0, 1);

l шестнадцатеричную (Hex) (0, 1,…, 9, A (10), B (11), C (12), D (13), E (14), F (15)).

Любое целое неотрицательное число, записанное в позиционной системе счисления:

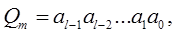
можно представить в виде степенного ряда (полинома):

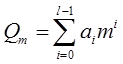
Максимальное целое число, которое может быть представлено в l разрядах:

Q_maх= m^l -1.

В ЭВМ для представления информации (данных) используется двоичная система счисления. Ее достоинства:

l используется только 2 символа (цифры) 0 и 1, что хорошо согласуется с техническими характеристиками цифровых схем, имеющих, как правило, 2 устойчивых состояния;

l в двоичной системе легко реализуются арифметические операции над числами.

Недостаток: длинные числа, которые неудобно записывать. Двоичное представление числа требует примерно в 3,3 раза большего числа разрядов, чем его десятичное представление.

В общем случае любое неотрицательное число (смешанную дробь), представленное в позиционной системе счисления, вида:

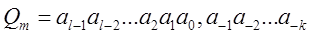
можно записать в виде полинома:

Здесь k – количество разрядов в дробной части числа, l – количество разрядов в целой части числа. Старший разряд имеет обозначение a_l-1, а младший – a_-k.

Минимальное значащее (не равное 0) число, которое можно записать в k разрядах дробной части:

Q_min=m^-k.

Имея в целой части числа l, а в дробной k разрядов, можно записать всего m^l+k разных чисел.

12. Позиционные системы счисления: перевод целых чисел из одной системы счисления в другую, арифметические действия над числами без знака.

Правило 1. Каждая цифра числа с основанием m представляется k цифрами системы счисления с основанием p и наоборот.

По этому правилу осуществляется перевод между 16-ричной и 2-ичной системами: 16¹=2⁴ и между 8-ричной и 2-ичной системами: 8¹=2³. В первом случае одна шестнадцатеричная цифра заменяется четырьмя двоичными цифрами (тетрадой) и наоборот. Во втором случае одна восьмеричная цифра заменяется тремя двоичными цифрами (триадой) и наоборот.

Правило 2. Перевод чисел из 8-ричной системы в 16-ричную систему и наоборот осуществляется через 2-ичную систему счисления.

Правило 3. Перевод чисел из любой системы счисления в десятичную осуществляется представлением этого числа либо в виде полинома (1), либо в виде схемы Горнера (2) и выполнением арифметических действий в десятичной системе счисления.

Правило 4. Для перевода целого десятичного числа в систему счисления с основанием p надо переводимое число и целочисленные промежуточные частные последовательно делить на основание p-й системы счисления до тех пор, пока не будет получено целое частное, меньшее основания p. Число в новой системе счисления запишется в виде остатков от деления, начиная с последнего частного, представляющего собой старшую цифру числа.

Для выполнения арифметических операций над числами, представленными в любой позиционной системе счисления надо пользоваться известными правилами арифметики.

l Сложение многоразрядных чисел начинается с младшего разряда и производится поразрядно с учетом единиц переноса из предыдущих разрядов.

l Вычитание двух многоразрядных чисел начинается с младших разрядов с учетом при необходимости переноса единиц (количество которых соответствует основанию системы счисления) из старших разрядов.

l Умножение и деление двух многоразрядных чисел в любой системе счисления выполняется по правилам десятичной системы счисления.

Существует еще одна арифметическая операция, часто выполняемая над двоичными числами – сложение по модулю 2.

Эта операция выполняется поразрядно и определяется следующим образом:

13. Позиционные системы счисления: перевод дробных чисел из одной системы счисления в другую.

Правило 5. Перевод правильных и неправильных дробей из одной системы счисления в другую, если основания этих систем являются степенями двойки, осуществляется по тем же правилам, что и для целых чисел.

Правило 6. Перевод правильных и неправильных дробей из любой системы счисления в десятичную осуществляется также как и для целых чисел, представлением этого числа либо в виде полинома (4), либо в виде схем Горнера (2, 5) и выполнением арифметических действий в десятичной системе счисления.

Правило 7. Для перевода правильных дробей в систему счисления с основанием p, последовательно умножают исходную дробь и дробные части промежуточных произведений на основание системы счисления p. Полученные в результате умножения целые числа произведения являются соответствующими разрядами дробного числа в системе счисления с основанием p.

В частном случае, если знаменатель правильной дроби представляет некоторую степень цифры 2, т.е.

то числитель a переводится в двоичную систему счисления как целое число, которое записывается в k разрядах после запятой.

Правило 8. Перевод неправильных дробей в систему счисления с основанием p выполняется отдельно для целой и дробной части числа по вышеизложенным правилам с последующим соединением этих частей в одну запись – неправильную дробь, представленную уже в новой системе счисления.

Дата добавления: 2015-04-24