Оценка надежности коэффициента корреляции

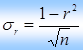Вероятностная оценка параметров корреляции производится по общим правилам проверки статистических гипотез, разработанным математической статистикой, в частности путем сравнения оцениваемой величины со средней случайной ошибкой оценки. то есть коэффициент корреляции находится в пределах r±3σ.

Применение коэф-та корр. если связь линейная.

8.4. Измерение связи неколичественных признаков (К-нт ассоциации, к-нт контингенции, к-нт сопряженности Пирсона, к-нт сопряженности Чупрова, к-нт корреляции рангов Спирмена, к-нт корреляции Фехнера)

Статистическая - связь, где воздействие отдельных факторов проявляется только как тенденция. Корреляция – мера зависимости переменных. Сила взаимосвязи данных.(Коэф-ты Пирсона, Фехнера, Спирмэна)

Пример:

Н0: мнение о кризисе не зависит от пола

Н1: пол влияет на отношение к кризису (предположение об отсутствии различий)

Коэффициент ассоциации:

A	B	A+B
C	D	C+D
A+C	B+D	A+B+C+D

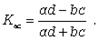
а, b, c, d - частоты взаимного сочетания (комбинации) двух альтернативных признаков

Kaс.кр=|0.5|. Если Kaс>Ккр –то подтв.гипотеза Н1, если наоборот-Н0.

Коэффициент контингенции:

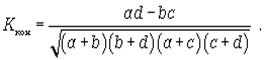
Если Kk>=0.3 подтверждается гип.Н1, если наоборот-Н0.

для одних и тех же данных коэффициент контингенции (изменяется от -1 до +1) всегда меньше коэффициента ассоциации. |Ka|>=Kk

Эти коэф-ты используются, если, например, необходимо исследовать тесноту зависимости между качественными признаками, каждый из которых представлен в виде альтернативных признаков.

Коэффициент сопряженности Чупрова

Коэффициент Чупрова измеряет взаимосвязь качественных неальтернативных признаков, измеренных по номинальной шкале. Подсчитывается по формуле:

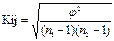
N1-число вариантов значений первого признака

N2-число вариантов знач.2-го признака

Коэф-т корреляции Пирсона:

Коэффициент корреляции Пирсона характеризует существование линейной зависимости между двумя величинами.

Интерпретация Пирсона: Отклонение признака-фактора от его среднего на величину стандартного отклонения в среднем приводит к отклонению признака-результата от своего среднего на величину r его стандартного отклонения.

Коэффициент корреляции Пирсона -1 ≤ Rxy ≤ 1. Rxy = -1Строгая отрицательная корреляция, Rxy = 1Строгая положительная корреляция, Rxy = 0Отсутствие корреляции

0,7 ≤ | Rxy | ≤ 1 Сильная корреляция, 0,5 ≤ | Rxy | ≤ 0,7 Средняя корреляция, 0,3 ≤ | Rxy | ≤ 0,5 Слабая корреляция, 0 ≤ | Rxy | ≤ 0,3 Незначимая корреляция

Меры тесноты парной связи:

Коэф-т Фехнера: мера тесноты связи виде отклонения разности числа пар совпадений и несовпадений признаков отклон. от среднего.

C – количество совпадающих знаков отклонений от средних

H – количество несовпадающих знаков отклонений от средних

C + H = n

Алгоритм расчета:

-расчет среднего для X и Y

-сравнение индивид.значений xi и yi со средними значениями с обязат.указаниями знака (+ или -). Если совпад., то относим к «С», если не совпад.,то к «Н».

-считаем кол-во совпад.или несовпад.

Коэффициент Спирмена:

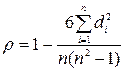Не параметр.показатель, с помощью кот.пытаемся выявить связи между рангами соответ.величин.

где di – разность рангов по обоим признакам для каждого объекта.

Дата добавления: 2015-04-24