Цели, виды

Множественная регрессия.

Уравнение множественной регрессии – аналитическая форма зависимости признака-результата от двух или более признаков-факторов.

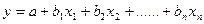
в - коэффициент регрессии

В уравнении множественной регрессии их называют условно чистыми коэффициентами. Их можно назвать чистыми коэффициентами, если бы в уравнении регрессии удалось включить все факторы определяющие результат..

Это невозможно пор нескольким причинам:

§ Ограниченный объем совокупности (число факторов должно 5-6 раз, идеально в 10 раз, меньше объема совокупности).

§ Не по всем факторам имеются данные.

§ Не все факторы имеют количественную оценку.

§ Не знаем о факторах, которые реально влияют на результат.

Интерпретация коэффициентов множественной регрессии аналогична интерпретации коэффициентов парной регрессии.

Коэффициент регрессии во множественном уравнении регрессии не равен коэффициенту регрессии в парном уравнении регрессии (при оценке влияния одного итого же фактора), так как в уравнении множественной регрессии величина коэффициента рассчитывается в условиях элиминирования влияния ряда факторов, включенных в уравнение.

При использовании методов корреляционно-регрессионного анализа можно выделить три группы решаемых практических задач.

4. Задачи, связанные с установлением наличия или отсутствия корреляционной зависимости. Решение этих задач предполагает расчет показателей корреляции.

5. Группа задач диктуется желанием управлять тем или иным объектом, или признаком через воздействие на факторы его определяющие. При этом строиться уравнение связи, называемое регрессионным, и производится ранжирование факторов по степени их влияния на результат.

6. Прогнозирование изменения того или иного явления или признака в условиях изменения соответствующих признаков-факторов. В основе решения данных задач лежат уравнения регрессии, которые в данном случае не являются самоцелью. Основное – это расчет прогнозируемых значений результативного признака с расчетом доверительных интервалов и указанием уровня доверительной вероятности.

Для решения всех задач используют методы корреляции и регрессии, но так как у них много общих вычислительных процедур, то принято говорить о корреляционно-регрессионном анализе.

Условия применения методов корреляционно-регрессионного анализа

6. Наличие статистической совокупности достаточно большого объема. Объем совокупности должен превышать в 5-6 раз (идеально в10 раз) число факторов, включенных в анализ.

7. Изучаемая совокупность должна быть однородна.

8. Независимость наблюдений и отсутствие мультиколлинеальности факторов.

9. Признаки, участвующие в анализе должны иметь количественное выражение.

10. Распределение единиц совокупности должно соответствовать нормальному закону распределения.

Дата добавления: 2015-04-24