Экономико-математическое моделирование. Экономико-математическое моделирование представляет собой процесс выражения экономических явлений математическими мо­делями

Экономико-математическое моделирование представляет собой процесс выражения экономических явлений математическими мо­делями. Экономическая модель — это схематичное представление экономического явления или процесса с использованием научной абстракции, отражение их характерных черт. Математические мо­дели — основное средство решения задач оптимизации любой дея­тельности. По своей сути эти модели — средство плановых расче­тов. Ценность их для экономического анализа и оптимизации реше­ний состоит в том, что они позволяют оценить напряженность плановых заданий, определить лимитирующую группу оборудова­ния, видов ресурсов, получать оценки их дефицитности и т.п. Мате­матическое моделирование экономических явлений и процессов дает возможность получить четкое представление об исследуемом объекте, охарактеризовать и количественно описать его внутреннюю струк­туру и внешние связи. Модель — условный образ объекта управле­ния /1/.

Экономико-математическая модель должна быть адекватной дей­ствительности, отражать существенные стороны и связи изучаемо­го объекта. Отметим принципиальные черты, характерные для по­строения экономико-математической модели любого вида. Процесс моделирования можно условно подразделить на три этапа: 1) ана­лиз теоретических закономерностей, свойственных изучаемому яв­лению или процессу и эмпирических данных о его структуре и особенностях; на основе такого анализа формируются модели; 2) определение методов, с помощью которых можно решить задачу; 3) анализ полученных результатов.

Важнейшим моментом первого этапа моделирования является четкая формулировка конечной цели построения модели, а также определение критерия, по которому будут сравниваться различные варианты решения. Такими критериями в системе менеджмента могут быть: а) максимизация полезного эффекта товара при ограни­чении совокупности затрат; б) максимизация прибыли фирмы при условии, что качество товара не снизится; в) снижение себестоимо­сти товара при условии, что его качество не снизится, затраты у потребителя не увеличатся; г) рост производительности труда, улуч­шение использования оборудования или материалов, повышение оборачиваемости оборотных средств при условии, что качество то­вара не снизится и другие критерии не ухудшатся. Таким образом, в качестве критерия оптимизации может быть целое или любой компонент прибыли, эффективности товара, объема рынка при ус­ловии, что другие компоненты при этом не ухудшатся.

Например, уравнение целевой функции (L) и система ограниче­ний по оптимизации прибыли фирмы (правда, у авторов нет огра­ничений по качеству товара) будет иметь следующий вид /1/:

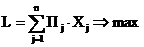(3.6)

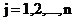, , , (3.7)

где х_j — количество производимой продукции j-го вида в нату­ральных измерениях;

П_j — прибыль, получаемая от производства единицы про­дукции j-го вида;

а_ij — норма расхода i-го производственного ресурса на про­изводство единицы j-го вида продукции;

ω_j — запасы i-го вида производственного ресурса на рас­сматриваемый период времени.

Не для всякой экономической задачи нужна собственная модель. Некоторые процессы с математической точки зрения однотипны и могут описываться одинаковыми моделями. Например, в линейном программировании, теории массового обслуживания и других су­ществуют типовые модели, к которым приводится множество конк­ретных задач.

Вторым этапом моделирования экономических процессов являет­ся выбор наиболее рационального математического метода для реше­ния задачи. Например, для решения задач линейного программиро­вания известно много методов: симплексный, потенциалов и др. Луч­шей моделью является не самая сложная и самая похожая на реальное явление, а та, которая позволяет получить самое рациональное реше­ние и наиболее точные экономические оценки. Излишняя детализа­ция затрудняет построение модели, а излишнее укрупнение модели приводит к потере существенной экономической информации, к не­адекватному отражению реальности.

Третьим этапом моделирования является всесторонний анализ результата, полученного при изучении экономического явления. Окончательным критерием достоверности и качества модели явля­ются практика, соответствие полученных результатов и выводов реальным условиям, экономическая содержательность полученных оценок. Если результаты не соответствуют реальным условиям, то необходим анализ причин несоответствия, в качестве которых могут быть недостоверность информации, несоответствие модели эконо­мическим условиям и др. По результатам анализа причин несоот­ветствия экономико-математическая модель корректируется и ре­шение задачи повторяется /1/.

49. Методы анализа количественного влияния факторов на изменение результативного показателя.

Метод дифференциального исчисления. Теоретической осно­вой для количественной оценки роли отдельных факторов в динамике результативного (обобщающего) показателя явля­ется дифференцирование.

В методе дифференциального исчисления предполагается, что общее приращение функций (результирующего показате­ля) различается на слагаемые, где значение каждого из них определяется как произведение соответствующей частной про­изводной на приращение переменной, по которой вычислена данная производная. Рассмотрим задачу нахождения влияния факторов на изменение результирующего показателя методом дифференциального исчисления на примере функции от двух переменных.

В методе дифференциального исчисления так называемый неразложимый остаток, который интерпрети­руется как логическая ошибка метода дифференцирования, просто отбрасывается. В этом состоит «неудобство» дифферен­цирования для экономических расчетов, в которых, как прави­ло, требуется точный баланс изменения результативного показателя и алгебраической суммы влияния всех факторов.

Индексный метод определения влияния факторов на обобща­ющей показатель. В статистике планировании и анализе хо­зяйственной деятельности основой для количественной оценки роли отдельных факторов в динамике изменений обобщающих показателей являются индексные модели.

Если обобщающий экономический показатель представля­ет собой произведение количественного (объемного) и качест­венного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксирует­ся на базисном уровне, а при определении влияния качествен­ного фактора количественный показатель фиксируется на уров­не отчетного периода.

Индексный метод позволяет провести разложение по фак­торам не только относительных, но и абсолютных отклонений обобщающего показателя.

Это отклонение образовалось под влиянием изменений чис­ленности работающих и производительности их труда. Чтобы определить, какая часть общего изменения объема выпуска продукции достигнута за счет изменения каждого из факторов в отдельности, необходимо при расчете влияния одного из них элиминировать влияние другого фактора.

Изложенный принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой качественный), а анализируемый по­казатель представлен как их произведение.

Теория индексов не дает общего метода разложения аб­солютных отклонений обобщающего показателя по факторам при числе факторов более двух.

Метод цепных подстановок. Этот метод заключается в получении ряда промежуточных значе­ний обобщающего показателя путем последовательной заме­ны базисных значений факторов на фактические. Разность двух промежуточных значений обобщающего показателя в цепи подстановок равна изменению обобщающего показателя, вы­званного изменением соответствующего фактора.

В общем виде имеем следующую систему расчетов по методу цепных подстановок.

Метод цепных подстановок, как и индексный, имеет недо­статки, о которых следует знать при его применении. Во-первых, результаты расчетов зависят от последовательности замена факторов; во-вторых, активная роль в изменении обо­бщающего показателя необоснованно часто приписывается влиянию изменения качественного фактора.

Задача точного определения роли каждого фактора в изменении обобщающего показателя обычным ме­тодом цепных подстановок не решается.

В этой связи особую актуальность приобретает поиск путей совершенствования точного однозначного определения роли отдельных факторов в условиях внедрения в экономическом анализе сложных экономико-математических моделей факторных систем.

Поиск путей совершенствования метода цепных подстано­вок (способа разниц) осуществлялся с двух позиций:

экономическое обоснование определенной последователь­ности подстановок путем исследования сущности хозяйствен­ных процессов и связей экономических факторов, при котором порядок расчетов определяется не.порядком расположения показателей в расчетной формуле, а их конкретным содержа­нием с выделением количественных и качественных факторов;

нахождение рациональной вычислительной процедуры (ме­тода факторного анализа), при которой устраняются условности и допущения и достигается получение однозначного ре­зультата величин влияния факторов.

Метод простого прибавления неразложимого остатка. Не находя достаточно полного обоснования, что делать с остат­ком, в практике экономического анализа стали использовать прием прибавки неразложимого остатка к качественному или количественному (основному или производному) фактору, а также делить этот остаток между двумя факторами поровну.

Описанный метод хотя и снимает проблему «неразложимого остатка», но связан с условием определения количественных и ка­чественных, факторов, что усложняет задачу при использовании больших факторных систем. Одновременно разложение общего прироста результативного показателя цепным методом зависит от последовательности подстановки. В этой связи получить однознач­ное количественное значение отдельных факторов без соблюдения дополнительных условий не представляется возможным.

Метод взвешенных конечных разностей. Этот метод состоит в том, что величина влияния каждого фактора определяется как по первому, так и по второму порядку подстановки, затем результат суммируется и от полученной суммы берется сред­няя величина, дающая единый ответ о значении влияния фак­тора. Если в расчете участвует больше факторов, то их значе­ния рассчитываются по всем возможным подстановкам.

метод взвешенных конечных разностей учиты­вает все варианты подстановок. Одновременно при усредне­нии нельзя получить однозначное количественное значение отдельных факторов. Этот метод весьма трудоемкий и по сравнению с предыдущим методом усложняет вычислитель­ную процедуру, так как приходится перебирать все возмож­ные варианты подстановок. В своей основе метод взбешен­ных конечных разностей идентичен (только для двухфактор­ной мультипликативной модели) методу простого прибавле­ния неразложимого остатка при делении этого остатка между факторами поровну.

С увеличением количества фактора, а значит, и количества подстановок, описанная идентичность методов не подтверждается.

Логарифмический метод. Этот метод состоит в том, что достигается логарифмически пропорциональное распределе­ние остатка по двум искомым факторам. В этом случае не требуется установления очередности действия факторов.

В более общем виде этот метод был описан еще А. Хумалом, который писал: «Такое разделение прироста произведе­ния может быть названо нормальным. Название оправдывает­ся тем, что полученное правило разделения остается в силе при любом числе сомножителей, а именно: прирост произведения разделяется между переменными сомножителями пропорцио­нально логарифмам их коэффициентов изменения».

Логарифмический метод в своей сути предусматривает получение логарифмических отношений, которые для расчленяющихся факторов будут примерно один­аковыми. Именно в этом и заключается недостаток описанного метода. Применение «смешанного» подхода в анализе кратных моделей факторных систем не решает проблемы получения изо­лированного значения из всего набора факторов, оказывающих влияние на изменение результативного показателя. Присутствие приближенных вычислений величин факторных изменений до­казывает несовершенство логарифмического метода анализа.

Метод коэффициентов. Этот метод основан на сопоставлении числового значения одних и тех же базисных экономических показателей при разных условиях.

Метод коэффициентов подкупает своей просто­той, но при точном выполнении алгебраических преобразо­ваний результат суммарного влияния факторов не совпадает с величиной изменения результативного показателя, получен­ного прямым расчетом.

Метод дробления приращений факторов. В анализе хозяй­ственной деятельности наиболее распространенными являют­ся задачи прямого детерминированного факторного анализа. С экономической точки зрения к таким задащм относится проведение анализа выполнения плана или динамики экономи­ческих показателей, при котором рассчитывается количествен­ное значение факторов, оказавших влияние на изменение ре­зультативного показателя. С математической точки зрения задачи прямого детерминированного факторного анализа представляют исследование функции нескольких переменных.

Дальнейшим развитием метода дифференциального исчис­ления явился метод дробления приращений факторных при­знаков» при котором следует вести дробление приращения Каждой из переменных на достаточно малые отрезки и осуще­ствлять пересчет значений частных производных при каждом (уже достаточно малом) перемещении в пространстве; Степень дробления принимается/такой, чтобы суммарная ошибка не влияла на точность экономических расчетов.

Ме­тод дробления приращений факторных признаков имеет пре­имущества перед методом, цепных подстановок. Он позволяет определить однозначно величину влияния факторов при зара­нее заданной точности расчетов, не связан с последователь­ностью подстановок и выбором качественных и количествен­ных показателей-факторов. Метод дробления требует соблю­дения условий дифференцируемости функции в рассматрива­емой области.

Интегральный метод оценки факторных влияний. Даль­нейшим логическим развитием метода дробления приращений факторных признаков стал интегральный метод факторного анализа. Этот метод основывается на суммировании прираще­ний функции, определенной как частная производная, умно­женная на приращение аргумента на бесконечно малых проме­жутках. При этом должны соблюдаться следующие условия:

1) непрерывная дифференцируемость функции, где в каче­стве аргумента используется экономический показатель;

2) функция между начальной и конечной точками элемен­тарного периода изменяется по прямой Г;

3) постояноство соотношения скоростей изменния факторов.

В реальных экономических процессах изменение факторов в области определения функции может происходить не по прямолинейному отрезку Г, а по некоторой ориентирован­ной кривой Г. Но так как изменение факторов рассматривает­ся за элементарный период (т.е. за минимальный отрезок времени, в течение которого хотя бы один из факторов полу­чит приращение), то траектория Г определяется единственно возможным способом— прямолинейным ориентированным отрезком Г, соединяющим начальную и конечную точки элементарного периода.

Можно выделить два направления практического исполь­зования интегрального метода в решении задач факторного анализа.

К первому направлению можно отнести задачи факторного анализа, когда не имеется данных об изменении факторов внутри анализируемого периода или от них можно абстраги­роваться, т.е. имеет место случай, когда этот дериод следует рассматривать как элементарный. В этом случае расчеты сле­дует вести по ориентированной прямой Г. Этот тип задач факторного анализа можно условно именовать статическим, так как при этом участвующие в анализе факторы харак­теризуются неизменностью положения по отношению к одно­му фактору, постоянством условий анализа измеряемых фак­торов независимо от нахождения их в модели факторной системы. Соизмерение приращений факторов происходит по отношению к одному выбранному для этой цели фактору.

К статическим типам задач интегрального метода фактор­ного анализа следует относить расчеты, связанные с анализом выполнения плана или динамики (если сравнение производит­ся с предшествующим периодом) показателей..

Ко второму направлению можно отнести задачи фактор­ного анализа, когда имеется информация об изменениях фак­торов внутри анализируемого периода и она должна прини­маться во внимание, т.е. случай, когда этот период в соответ­ствии с имеющимися данными разбивается на ряд элементар­ных.

К динамическим типам задач интегрального метода фак­торного анализа, следует относить расчеты, связанные с анали­зом временных рядов экономических показателей. В этом слу­чае можно подобрать, хотя и приближенно, уравнение, описы­вающее поведение анализируемых факторов во времени за весь рассматриваемый период. При этом в каждом разбива­емом элементарном периоде может быть принято индивиду­альное значение, отличное от других.

Интегральный метод факторного анализа находит применение в практике детермивировааного экономического анали­за.

Статический тип задач интегрального метода факторного анализа — наиболее разработанный и распространенный тип задач в детерминированном экономическом анализе хозяй­ственной деятельности управляемых объектов.

В сравнении с другими методами рациональной вычис­лительной процедуры интегральный метод факторного анали­за устранил неоднозначность оценки влиянии факторов и по­зволил получить наиболее точный результат. Результаты рас­четов по интегральному методу существенно отличаются от того, что дает метод цепных подстановок или модификации последнего. Чем больше величина изменений факторов, тем разница значительнее.

Метод цепных подстановок (его модификации) в своей основе слабее учитывает соотношение величин измеряемых факторов. Чем больше разрыв между величинами приращений факторов, входящих в модель факторной системы, тем сильнее реагирует на это интегральный метод факторного анализа.

В отличие от цепного метода в интегральном методе действует логарифмический закон перераспределения фактор­ных нагрузок, что свидетельствует о его больших достоин­ствах. Этот метод объективен, поскольку исключает какие-либо предложения о роли факторов до проведения анализа. В отличие от других методов факторного анализа при ин­тегральном методе соблюдается положение о независимости факторов.

Важной особенностью интегрального метода факторного анализа является то, что ов дает общий подход к решению задач самого разного вида независимо от количества элемен­тов, входящих в модель факторной системы, и формы связи между ними. Вместе с тем в целях упрощения вычислительной процедуры разложения приращения результирующего показателя на факторы следует придерживаться других групп (видов) факторных моделей: мультипликативных и кратных. Вычис­лительная процедура интегрирования одна и та же, а получа­емые конечные формулы расчета факторов различны.

Формирование рабочих формул интегрального метода для мультипликативных моделей. Применение интегрального ме­тода факторного анализа в детерминированнбм экономичес­ком анализе наиболее полно решает проблему получения од­нозначно определяемых величин влияния факторов.

Появляется потребность в формулах расчета влияния фак­торов для множества видов моделей факторных систем (фун­кций).

Выше было установлено, что любую модель конечной фак­торной системы можно привести к двум видам — мультип­ликативной и кратной. Это условие предопределяет то, что исследователь имеет дело с двумя основными видами моделей факторных систем, так как остальные модели — это их раз­новидности.

Операция вычисления определенного интеграла по задан­ной подынтегральной функции и заданном интервалу интег­рирования выполняется по стандартной программе, заложен­ной в память машины. В этой связи задача сводится лишьк построению подынтегральных выражений, которые зависят от вида функции или модели факторной системы.

Для облегчения решения задачи построения подынтеграль­ных выражений в зависимости от вида модели факторной системы (мультипликативные или кратные) предложим матри­цы исходных значений для построения подынтегральных выра­жений элементов структуры факторной системы. Принцип, заложенный в матрицах, позволяет построить подынтеграль­ные выражения элементов структуры факторной системы для любого набора элементов модели конечной факторной систе­мы. В основном построение подынтегральных выражений эле­ментов структуры факторной системы — процесс индивиду­альный, и в случае, когда число элементов структуры измеря­ется большим количеством, что в экономической практике является редкостью, исходят из конкретно заданных условий.

При формировании рабочих формул расчета влияния фак­торов в условиях применения ЭВМ пользуются следующими правилами, отражающими механику работы с матрицами: подынтегральные выражения элементов структуры факторной системы для мультипликативных моделей строятся путем про­изведения полного набора элементов значений, взятых по каж­дой строке матрицы, отнесенных к определенному элементу структуры факторной системы с последующей расшифровкой значений., приведенных справа и внизу матрицы исходных значений.

Использование рабочих формул значительно расширяется в детерминированном цепном анализе, при котором выявлен­ный фактор может быть ступенчато разложен, на составля­ющие как бы в другой плоскости анализа.

Примером детерминированного цепного факторного ана­лиза может/быть внутрихозяйственный анализ производствен­ного объединения, при котором оценивается роль каждой про­изводственной единицы в достижении лучшего результата в целом по объединению.

50. Метод корреляционно-регрессионного анализа.

Применяются для определения зависимости изменения цены от изменения технико-экономических параметров продукции, относящейся к данному ряду, построения и выравнивания ценностных соотношений:

где Х1, Х2,... Xn — параметры изделия.
Количественная зависимость находится на основе метода регрессионного анализа. При этом могут быть получены различные уравнения регрессии: линейное, степенное, параболическое и т. д.

Если цены на уже включенные в параметрический ряд изделия были получены таким же методом, то использовать данный способ нельзя, так как нарушается одно из условий применения регрессионного анализа, — условие независимости наблюдений.

Тем не менее, данный метод можно применять для прогнозной цены.

В качестве общего вывода по поводу применения параметрических методов следует отметить, что они крайне несовершенны и самостоятельно для формирования цены, как правило, не применяются. Основным недостатком использования данных методов является то, что они учитывают не все потребительские свойства изделий и полностью игнорируют спрос и предложение.

51. Методика факторного анализа.

од факторным анализом понимается методика комплексного и системного изучения и измерения воздействия факторов на величину результативных показателей.

Различают следующие типы факторного анализа:

детерминированный (функциональный) и стохастический (корреляционный);

прямой (дедуктивный) и обратный (индуктивный);

одноступенчатый и многоступенчатый;

статический и динамичный;

ретроспективный и перспективный (прогнозный).

Детерминированный факторный анализ представляет собой методику исследования влияния факторов, связь которых с результативным показателем носит функциональный характер, т.е. результативный показатель может быть представлен в виде произведения, частного или алгебраической суммы факторов.

Стохастический анализ является методикой исследования факторов, связь которых с результативным показателем в отличие от функциональной является неполной (вероятностной корреляционной). Если при функциональной (полной) зависимости с изменением аргумента всегда происходит соответствующее изменение функции, то при корреляционной связи изменение аргумента может дать несколько значений прироста функции в зависимости от сочетания других факторов, определяющих данный показатель. Например, производительность труда при одном и том же уровне фондовооруженности может быть неодинаковой на разных предприятиях. Это зависит от оптимальности сочетания других факторов, воздействующих на этот показатель.

При прямомфакторном анализе исследование ведется дедуктивным способом – от общего к частному. Обратный факторный анализ осуществляет исследование причинно-следственных связей способом логичной индукции – от частных, отдельных факторов к обобщающим.

Факторный анализ может быть одноступенчатым и многоступенчатым. Первый тип используется для исследования факторов только одного уровня (одной ступени) подчинения без их детализации на составные части. Например, у=а × в. При многоступенчатом факторном анализе проводится детализация факторов a и b на составные элементы с целью изучения их поведения. Дета­лизация факторов может быть продолжена и дальше. В данном случае изучается влияние факторов различных уровней соподчиненности.

Необходимо различать также статический и динамический факторные анализы. Первый вид применяется при изучении влияния факторов на результативные показатели на соответствующую дату. Другой вид представляет собой методику исследования причинно-следственных связей в динамике.

И наконец, факторный анализ может быть ретроспективным, который изучает причины прироста результативных показателей за прошлые периоды, и перспективным, который исследует поведение факторов и результативных показателей в перспективе.

Основными задачами факторного анализа являются следующие:

1. Отбор факторов, которые определяют исследуемые результативные показатели.

2. Классификация и систематизация их с целью обеспечения возможностей системного подхода.

3. Определение формы зависимости между факторами и результативным показателем.

4. Моделирование взаимосвязей между результативным и факторными показателями.

5. Расчет влияния факторов и оценка роли каждого из них в изменении величины результативного показателя.

6. Работа с факторной моделью (практическое ее использование для управления экономическими процессами).

Отбор факторов для анализа того или другого показателя осуществляется на основе теоретических и практических знаний, приобретенных в этой отрасли. При этом обычно исходят из принципа: чем больший комплекс факторов исследуется, тем более точными будут результаты анализа. Вместе с тем необходимо иметь в виду, что если этот комплекс факторов рассматривается как механическая сумма, без учета их взаимодействия, без выделения главных, определяющих, то выводы могут быть ошибочными. В экономическом анализе взаимосвязанное исследование влияния факторов на величину результативных показателей достигается с помощью их систематизации, что является одним из основных методологических вопросов этой науки.

Важным методологическим вопросом в факторном анализе является определение формы зависимости между факторами и результативными показателями: функциональная она или стохастическая, прямая или обратная, прямолинейная или криволинейная. Здесь используются теоретический и практический опыт, а также способы сравнения параллельных и динамичных рядов, аналитических группировок исходной информации, графический метод и др.

Моделирование экономических показателей (детерминированное и стохастическое) также представляет собой сложную методологическую проблему в факторном анализе, решение которой требует специальных знаний и практических навыков в этой отрасли, почему этому вопросу в данном курсе и уделяется много внимания.

Самый главный методологический аспект в экономическом анализе – расчет влияния факторов на величину результативных показателей, для чего в анализе используется целый арсенал способов, сущность, назначение, сфера применения которых и процедура расчетов рассматриваются в следующих главах.

И наконец, последний этап факторного анализа – практическое использование факторной модели для подсчета резервов прироста результативного показателя, для планирования и прогнозирования его величины при изменении производственной ситуации.

52. Методы линейного программирования.

Методы линейного программирования применяются для решения многих экстремальных задач, с которыми довольно часто приходится иметь дело в экономике. Решение таких задач сводится к нахождению крайних значений (максимума и минимума) некоторых функций переменных величин.

Линейное программирование основано на решении системы линейных уравнений (с преобразованием в уравнения и неравенства), когда зависимость между изучаемыми явлениями строго функциональна. Для него характерны математическое выражение переменных величин, определенный порядок, последовательность расчетов (алгоритм), логический анализ. Применять его можно только в тех случаях, когда изучаемые переменные величины и факторы имеют математическую определенность и количественную ограниченность, когда в результате известной последовательности расчетов происходит взаимозаменяемость факторов, когда логика в расчетах, математическая логика совмещаются с логически обоснованным пониманием сущности изучаемого явления.

С помощью этого метода в промышленном производстве, например, исчисляется оптимальная общая производительность машин, агрегатов, поточных линий (при заданном ассортименте продукции и иных заданных величинах), решается задача рационального раскроя материалов (с оптимальным выходом заготовок). В сельском хозяйстве он используется для определения минимальной стоимости кормовых рационов при заданном количестве кормов (по видам и содержащимся в них питательным веществам). Задача о смесях может найти применение и влитейном производстве (состав металлургической шихты). Этим же методом решаются транспортная задача, задача рационального прикрепления предприятийпотребителей к предприятиямпроизводителям. Все экономические задачи, решаемые с применением линейного программирования, отличаются альтернативностью решения и определенными ограничивающими условиями. Решить такую задачу — значит выбрать из всех допустимо возможных (альтернативных) вариантов лучший, оптимальный. Важность и ценность использования в экономике метода линейного программирования состоят в том, что оптимальный вариант выбирается из весьма значительного количества альтернативных вариантов. При помощи других способов решать такие задачи практически невозможно.

В качестве примера рассмотрим решение задачи рациональности использования времени работы производственного оборудования.

В соответствии с оперативным планом участок шлифовки за первую неделю декабря выпустил 500 колец для подшипников типа А, 300 колец для подшипников типа Б и 450 колец для подшипников типа В. Все кольца шлифовались на двух взаимозаменяемых станках разной производительности. Машинное время каждого станка составляет 5000 мин. Трудоемкость операций (в минутах на одно кольцо) при изготовлении различных колец характеризуется следующими данными (6.5).

Таблица 6.5

Следует определить оптимальный вариант распределения операций по станкам и время, которое было бы затрачено при этом оптимальном варианте. Задачу выполним симплексным методом.

Для составления математической модели данной задачи введем следующие условные обозначения: дс,,, х, — соответственно количество колец для подшипников типов А, Б, В, производимых на станке I;, х, х, — соответственно количество колец для подшипников типов А, Б, В, производимых на станке П. Линейная форма, отражающая критерий оптимальности, будет иметь вид:

min а(х) = 4х, + 10л:+10л:з + 6х+20х

при ограничениях

4х,+ 10x^5000

+ 8х+20х^5000

х, +х= 500

= 300

= 450

Преобразуем условие задачи введением дополнительных (вспомогательных) и фиктивных переменных. Условие запишем так:

min <х(х) = 4х + \0х+\0х + 6х + 8х + 20х+ + Мх + Мх

Система уравнений, отражающая ограничительные условия машинного времени и количество произведенной продукции:

4х, + 10л: + lOxj+ = 5000

+ Sx + 20x + x=5000

+ х=

= 300

л^0,у=1,

Решение этой задачи представлено в 6.6. Оптимальный вариант получен на седьмом этапе (итерации). Если бы на станке I производилось 125 колец подшипников типа А, 450 колец подшипников типа В, на станке II — 375 колец подшипников типа А и 300 колец подшипников типа Б, то при такой загрузке оборудования было бы высвобождено 350 мин машинного времени станка II. Общие затраты времени по оптимальному варианту составили бы 9650 мин, тогда как фактически затрачено 10000 мин машинного времени.

Весьма типичной задачей, решаемой с помощью линейного программирования, является транспортная задача. Ее смысл заключается в минимизации грузооборота при доставке товаров широкого потребления от производителя к потребителю, с оптовых складов и баз в розничные торговые предприятия. Она решается симплексметодом или распределительным методом.

Решение транспортной задачи распределительным методом было дано в третьем издании учебника «Теория экономического анализа» («Финансы и статистика», 1996).

Таблица 6.6

Решение задачи рациональности использования станков симплексным методом

Дата добавления: 2015-04-24