Однородный поток

Основная статья: Поток однородных событий

Поток заявок однороден, если:

§ все заявки равноправны,

§ рассматриваются только моменты времени поступления заявок, т.е. факты заявок без уточнения деталей каждой конкретной заявки.

[править]Поток без последействия

Поток без последействия, если число событий любого интервала времени (, ) не зависит от числа событий на любом другом непересекающемся с нашим (, ) интервале времени.

[править]Стационарный поток

Поток заявок стационарен, если вероятность появления n событий на интервале времени (, ) не зависит от времени , а зависит только от длины этого участка.

[править]Простейший поток

Однородный стационарный поток без последействий является простейшим, потоком Пуассона.

Число событий такого потока, выпадающих на интервал 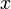, распределено по Закону Пуассона:

Пуассоновский поток заявок удобен при решении задач ТМО. Строго говоря простейшие потоки редки на практике, однако многие моделируемые потоки допустимо рассматривать как простейшие.

[править]Мгновенная плотность

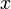Мгновенная плотность (интенсивность) потока равна пределу отношения среднего числа событий, приходящихся на элементарный интервал времени (, ) к длине интервала (), когда последний стремится к нулю.

или, для простейшего потока,

где 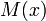равно математическому ожиданию числа событий на интервале .

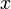[править]Формула Литтла

Среднее число заявок в системе равно произведению интенсивности входного потока на среднее время пребывания заявки в системе.

56. Матричные методы анализа.

матричный анализ — метод исследования взаимосвязей между экономическими объектами с помощью их матричного моделирования. * * * МАТРИЧНЫЙ АНАЛИЗ МАТРИЧНЫЙ АНАЛИЗ, метод исследования взаимосвязей между экономическими объектами с помощью их матричного моделирования

Матричные методы анализа, основанные на линейной и векторноматричной алгебре, применяются для изучения сложных и высокоразмерных структур как на отраслевом уровне, так и на уровне предприятий и их объединений.

Применение матричных методов покажем на следующем примере.

Два цеха предприятия выпускают продукцию двух видов: первый цех — продукцию 1-го вида, второй цех — продукцию 2-го вида. Часть выпускаемой продукции идет на внутреннее потребление, остальная является конечным продуктом. Требуется выявить распределение между цехами продукции, идущей на внутреннее потребление (xij), и общие (валовые) объемы выпускаемой продукции (л:),если заданы параметры прямых затрат (А) и конечного продукта (у

Элементы матрицы прямых затрат А представляют собой коэффициенты прямых затрат продукции /-го вида на производство единицы продукции /-го вида. В нашем примере эти коэффициенты будут такими:

Элементы векторстолбца у определяют величину конечного продукта, идущего на внешнюю реализацию:

н;;)=РДля определения валового (общего) выпуска продукции 1-го и 2-го видов воспользуемся следующей формулой:

х = (Е—А)-*у,

где Е — единичная матрица; (ЕА)"

матрица полных затрат;

(ЕА) =

Определитель этой матрицы равен:

ГГ-(-10-Н-4-) 16 1

25~40~

Получим обратную матрицу В = (Е—А) методом алгебраических дополнений.

Матрица алгебраических дополнений D формируется следующим образом:

,=(-1) у =у, d = ()=-;

V d I d'

57. Теория нечетких множеств.

Теория нечётких множеств (Заде) — это расширение классической теории множеств, используется в нечёткой логике. Впервые предложена Лотфи А. Заде в 60-х годах XX века.

В классической теории множеств принадлежность элементов множеству оценивается в бинарных терминах в соответствии с чётким условием — элемент либо принадлежит, либо нет данному множеству. Напротив, теория нечётких множеств разрешает градуированную оценку отношения принадлежности элементов множеству; то есть это отношение описывается при помощи функции принадлежности . Нечёткие множества — это расширение классической теории множеств, поскольку на некотором множестве функция принадлежности может действовать так же, как индикаторная функция, отображая все элементы либо в 1, либо в 0, как в классическом варианте.

[править]Определение

Нечёткое множество на классическом множестве 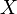определяется как следующее:

Функция принадлежности количественно градуирует принадлежность элементов 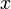фундаментальному множеству 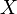. Отображение элемента в значение 0 означает, что элемент не принадлежит данному множеству, значение 1 описывает полной принадлежности элемента множеству. Значения, лежащие строго между 0 и 1, характеризуют «нечёткие» элементы.

Нечёткое множество и чёткое (crisp) классическое множество

Следующие соотношения выполнены для значений функции принадлежности

58. Способы сравнения в анализе хозяйственной деятельности.

Дата добавления: 2015-04-24