Свойства электрического заряда

Заряд бывает двух видов, называемых положительным и отрицательным:

заряды одного вида отталкиваются друг от друга, заряды разных видов - притягиваются, причем сила отталкивания равна по модулю силе притягивания;

число положительных и отрицательных зарядов во Вселенной одинаковое.

Полный электрический заряд изолированной системы сохраняется. Закон Кулона и пpинцип супеpпозиции полей. Электpостатика лекции и конспекты по физике

Электрический заряд релятивистски инвариантен, т. е. его величина не зависит от скорости системы отсчета, как бы велика она ни была.

Величина заряда может принимать только дискретные значения:

минимальный заряд частицы e = 1.60·1019 Кл;

любой заряд q кратен минимальному, т.е. q=Ne, где N - целое число;

минимальные положительный и отрицательный заряды равны по абсолютной величине.

3.Сила Лоренса. Движение зарядов в электромагнитном поле

Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поле действует на точечную заряженную частицу. Иногда, силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1] иначе говоря, со стороны электрического 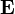и магнитного 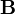полей в СИ:

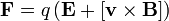
Мы же рассмотрим движение в однородном магнитном поле, когда электрического поля нет. Эту задачу мы уже решали. Одним из ре­шений было движение частиц по окружности. Магнитная сила

qv X В всегда действует под прямым углом к направлению движения, так что производная dp/dt перпендикулярна р и равна по величине vp/R, где R — радиус окружности, т. е.

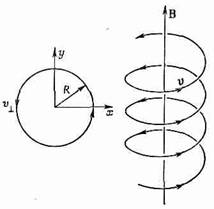
Фиг. 29.1. Движение частицы в однородном магнитном поле.

Таким образом, радиус круговой орбиты равен

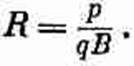
4.Напряжённость поля неподвижного точечного заряда. Свойство поля

Напряженность поля точечного заряда. Используя закон Кулона (1.1) найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:

(1.2)

В этой формуле r – радиус-вектор, соединяющий заряды q и q _пр. Из (1.2) следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.

Главное свойство электрического поля — это способность действовать на электрические заряды (как неподвижные, так и движущиеся) с некоторой силой.

5.Электростатическое поле системы зарядов. Принцип супер позиции. Поле электростатического диполя.

Принцип суперпозиции:в классической физике: допущение, согласно которому результирующий эффект от нескольких независимых воздействий представляет собой сумму эффектов, вызываемых каждым воздействием в отдельности. Справедлив для систем или полей, описываемых линейными уравнениями; важен в механике, теории колебаний и волн, теории физических полей.

Электрическим диполем называется система двух одинаковых по величине, но разноименных точечных зарядов, расстояние между которыми l значительно меньше расстояния до тех точек, в которых определяется поле системы (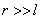) (рис. 1.6).

Здесь 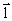называют плечо диполя – вектор, направленный от отрицательного заряда к положительному и численно равный расстоянию между зарядами.

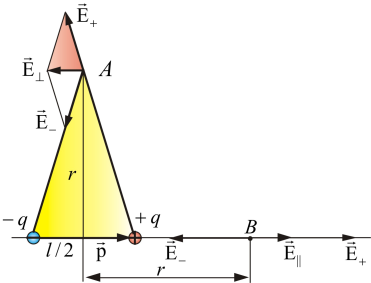
Рис. 1.6

Пример 1. Найдем Е^ в точке А на прямой, проходящей через центр диполя и перпендикулярной к оси (рис. 1.6)

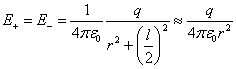
(т.к. )

(1.5.1)

Из подобия заштрихованных треугольников можно записать:

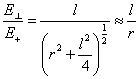
отсюда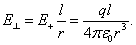

(

(1.5.2)

Обозначим вектор: – электрический момент диполя (или д ипольный момент) – произведение положительного заряда диполя на плечо . Направление совпадает с направлением, т.е. от отрицательного заряда к положительному. Тогда, учитывая что 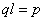получим:

,

или

(1.5.3)

Пример 2. На оси диполя, в точке В (рис. 1.6):

,

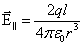или

(

(1.5.4)

Пример 3. В произвольной точке С (рис. 1.7).

Рис. 1.7

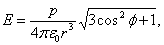
6. Определинение потока вектора напряжённости электростатического поля.

Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности N_E.

Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным (рис.13.4).

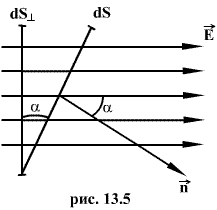
Поток напряженности через такую элементарную площадку будет равен по определению(рис.13.5).

где - угол между силовой линией и нормалью 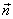к площадке dS; - проекция площадки dS на плоскость, перпендикулярную силовым линиям. Тогда поток напряженности поля через всю поверхность площадки S будет равен

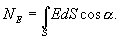
(13.4)

Так как 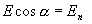, то

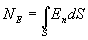
(13.5)

где 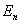- проекция вектора 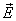на нормаль и к поверхности dS.

7.Теорема Остроградсково-Гауса

Пусть в некоторой области пространства известно векторное поле напряженности электростатического поля 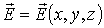. Допустим, что в окрестности фиксированной точки пространства имеется элемент поверхности площади 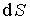, ориентацию которого можно задать с помощью вектора единичной (безразмерной) нормали 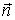к этому элементу поверхности. Поскольку элемент поверхности является двусторонним объектом, то направление нормали можно выбрать произвольно. Введем в рассмотрение объект

,

(1.42)

вектор элемента площади поверхности. В соответствии с (1.42) этот вектор численно равен площади элемента поверхности, имеет размерность площади и направлен вдоль 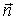, то есть вдоль нормали к элементу поверхности.

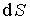Элемент потока вектора через площадку по определению равен скалярному произведению вектора и вектора :

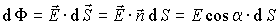.	(1.43)

8.Теорема Остроградсково-Гауса и её применение для нахождения напряжённости элекстратическово поля однородно заряженной бесконечной нити

Дата добавления: 2015-04-24